2.1.5 Метод эквивалентного генератора

Пусть какая-либо ветвь ab электрической цепи, в которой необходимо определить ток, содержит сопротивление Z_ab. Тогда по отношению к этой ветви вся остальная часть электрической цепи может быть заменена одним эквивалентным генератором с ЭДС и внутренним сопротивлением (рисунок 31).

Рисунок 31

Искомый ток равен

Параметры эквивалентного генератора , можно определить следующим образом. Величина равна напряжению на зажимах разомкнутой ветви (напряжение холостого хода):

Величину можно найти двумя способами:

1. Сопротивление равно входному сопротивлению цепи относительно зажимов а и b исходной схемы, из которой исключены все источники электрической энергии. При этом участок ветви, в котором был источник ЭДС, замыкается накоротко, а участок с источником тока размыкается (рисунок 32).

2. Замкнём участок ab накоротко (рисунок 33) и определим (опытным или расчётным путём) ток короткого замыкания . Тогда

Рисунок 32 Рисунок 33

Пример. Найдем ток в цепи (рисунок 29) методом эквивалентного генератора. Разомкнем ветвь с сопротивлением Z₅ и определим величину (рисунок 34).

Рисунок 34

Предположим сначала, что токи в ветвях схемы нам известны. Составим уравнение по второму закону Кирхгофа так, чтобы в него входило искомое напряжение.

Тогда

Для расчетов токов можно воспользоваться известными способами расчета электрических цепей. Найдем их методом контурных токов:

Найдем величину Z_r двумя способами.

1. Исключив из схемы источники ЭДС (рисунок 35), найдем величину входного сопротивления Z_r относительно зажимов ab. Для этого заменим треугольник сопротивлений Z₁, Z₂, Z₄ эквивалентной звездой Z_7, Z₈, Z₉ (рисунок 36):

Тогда получим

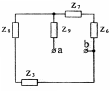
Рисунок 35 Рисунок 36

2. Замкнем накоротко зажимы ab (схема рисунок 37) и найдем ток короткого замыкания методом контурных токов:

Рисунок 37

Тогда получим

окончательно искомый ток равен

2.2 Пример выполнения задания

В качестве примера рассчитаем электрическую схему (рисунок 38), для которой Z₁=20+j30 Ом; Z₂= -j45 Ом; Z₃=10 Ом; Z₄=50-j10 Ом; Z₅=j80 Ом; Z₆=30+j60 Ом; Z₇=75-j25 Ом; Z₈=20 Ом.

2.2.1. Расчет методом контурных токов

Для определения независимых контуров воспользуемся топологическими понятиями, определяющими способ соединения элементов. На топологической схеме каждую ветвь электрической цепи заменяют отрезком линии, при этом ветви с источником ЭДС сохраняются, а ветви с источников тока не входят в топологическую схему. Условное изображение схемы, где каждая ветвь заменяется отрезком линии, называют графом электрической цепи. Дерево графа – это любая совокупность ветвей графа, соединяющих все его узлы без образования контуров. Ветви графа, не входящие в состав дерева, называют ветвями – связями графа.

Рисунок 38

Рисунок 39

Для получения независимого контура необходимо к дереву графа добавить какую-либо одну ветвь связи. Так, на рисунке 39 показан граф электрической цепи (рисунок 38), включающий дерево графа (сплошные линии) и ветви связи (пунктирные линии). Независимые контуры образованы ветвями дерева и ветвями связи с номерами 1, 5, 7, 4 и 8. Соответствующие контурные токи обозначены

Уравнения для определения контурных токов имеют вид:

Подставив численные значения, получим:

В результате решения этой системы на ЭВМ получим:

Искомые токи определяем следующим образом: