2.1.3 Метод узловых потенциалов

Если в разветвлённой электрической цепи число узлов без единицы меньше, чем число независимых контуров (k-1)<[n-(k-1)], удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы алгебраических уравнений (k-1)-го порядка относительно неизвестных потенциалов (узловых потенциалов). При этом потенциал одного из узлов схемы полагают равным нулю.

Уравнения с узловыми потенциалами вытекают из первого закона Кирхгофа. После нахождения неизвестных потенциалов определяют токи в ветвях по закону Ома.

Уравнения, входящие в систему, являются однотипными и для m-го узла имеют следующий вид:

где – сумма проводимостей всех ветвей, сходящихся в m-ом узле, ;

– проводимость ветви, соединяющей узел m c узлом q. Если между какими-либо узлами нет ветви, то соответствующая проводимость равна нулю;

– ЭДС источников, расположенных в ветви между узлами m или q.

При этом ЭДС, направленные к узлу m (относительно которого составляется уравнение), берутся положительными, а направленные от этого узла – отрица­тельными.

Составим систему уравнений для схемы Рисунок 28, полагая :

где

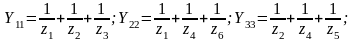
Рисунок 28

После определения потенциалов находим токи по закону Ома:

Если ветвь содержит источник тока, то её проводимость равна нулю, т.к. внутреннее сопротивление источника тока равно бесконечности. Если к m-му узлу подтекает ток от источника тока, то он должен быть включен в правую часть уравнения со знаком «плюс», если утекает, то со знаком «минус». Так, для цепи (рисунок 29) система уравнений имеет вид при :

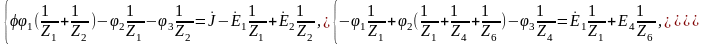
Рисунок 29

2.1.4 Баланс мощностей

В любой электрической цепи по закону сохранения энергии количество выра­батываемой за единицу времени энергии источников должно равняться мощности потребителей:

Р_ист=Р_потр, Q_ист=Q_потр.

Любое нарушение этих соотношений указывает на неточность проведённых вычислений.

Активную и реактивную мощности источников можно найти как действительную и мнимую части полной комплексной мощности источников:

где – сопряженный комплекс тока

Если направление тока совпадает с направлением источника ЭДС, то произве­дение входит в левую часть равенства со знаком «плюс», в противном случае – со знаком «минус».

Если электрическая цепь содержит источник тока j, то

где – напряжение на зажимах источника тока.

Активная мощность потребителей:

где I_q – действующее значение тока q-й ветви, содержащей активное сопротивление R_q.

Реактивная мощность потребителей:

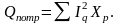
Для индуктивности произведение I²X_L входит в сумму со знаком «плюс», для емкости I²X_c – со знаком «минус».

Пример составления баланса мощности

В цепи (рисунок 30) с параметрами:

R₁=15 Ом; R₂=8 Ом; R₃=20 Ом;

X_L=20 Ом; X_C1 =10 Ом; X_C2 =15 Ом,

Рисунок 30

расчетным путем найдены токи:

Для составления баланса мощности найдем напряжение на зажимах источника тока (по второму закону Кирхгофа):

Тогда

Отсюда

Р_ист=8605,18 Вт; Q_ист=-2420,56 ВАр.

Найдём активную мощность потребителей:

Р_потр=13,758^{2 .} 15+21,695^{2 .} 8+10^{2 .} 20=8604,62 Вт.

Реактивная мощность потребителей:

Q_потр=13,758^{2 .} 20 - 21,695^{2 .} 10 - 10^{2 .} 15= -2421,08 BАp.

Баланс мощности выполняется в пределах допустимой погрешности расчета (до 3%).