2.4.Выбор динамической модели и определение её параметров

В качестве динамической модели механизма выбирается динамическая модель с вращательным звеном приведения. В качестве звена приведения выбирается звено 8 исходного механизма. К звену приведения прикладывается суммарный приведенный момент , а момент инерции относительно оси вращения равен суммарному приведенному моменту инерции .

Рис. 8. Динамическая модель

М_^пр - суммарный приведенный момент - параметр ди­намической модели, который является эквивалентом задан­ной нагрузки, приложенной к механизму;

J_^пр- суммарный приведенный момент инерции - является эквивалентом всей инерционности механизма;

Условием приведения сил является равенство работ на возможном перемещении, условием приведения масс является равенство кинетических энергий.

Выделяют моменты инерции первой и второй группы:

J_^ПР.= J_I^ПР. + J_II^ПР., где

J_I^ПР.- сумма приведенных моментов инерции звеньев, связанных со звеном приведения посто­янным передаточным отношением.

J_II^{ПР. .}- сумма приведенных моментов инерции звеньев, связанных со звеном приведения пере­менным передаточным отношением.

2.5.Построение графиков приведенных моментов инерции звеньев II группы

_{Звенья механизма делят на две группы. В первую группу входит начальное звено и все звенья, связанные с ним постоянным передаточным отношением. Приведенные моменты инерции звеньев первой группы – постоянны, их значение не зависит от положения механизма. Их сумма обозначается} . Ко второй группе относятся все остальные звенья механизма. Приведенные моменты инерции звеньев этой группы – переменны, они зависят от положения механизма. Их сумма обозначается как _.

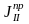_{Следовательно,}

_{Приведенный момент инерции в общем виде определяется по формуле:}

_{Где и - передаточные функции (аналоги скоростей).}

Полученные значения и графики приведены в Приложении 1.

2.6.Определение суммарного приведенного момента

Закон движения механизма определяется характером сил и моментов, приложенных к его звеньям. Все внешние силы, действующие на машину, делятся на движущие силы (момент движущих сил ) и силы сопротивления (момент сил сопротивления ).

Механизм работает в установившемся режиме (кинетическая энергия или обобщённая скорость являются периодическими функциями времени). Значит работа сил сопротивления за цикл равна по модулю работе, которая совершается движущими силами.

Так как приведенный момент движущих сил , определяем по формуле:

= -444.732 Н*м

Полученные значения и графики приведены в Приложении 1.

2.7.Определение суммарной работы

Суммарную работу всех сил можно определить путем интегрирования суммарного приведенного момента _.

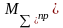Полученные значения и графики приведены в Приложении 1.

2.8.Определение кинетической энергии II группы звеньев

Кинетическая энергия механизма

Учитывая 1ое допущение Мерцалова .

Полученные значения и графики приведены в Приложении 1.