Ряды динамики

1. Виды динамических рядов.

2. Система показателей для анализа, рядов динамики.

3. Средние показатели в рядах динамики.

4. Методы обработки рядов динамики. Прогнозирование в рядах динамики

5. Сезонные колебания в рядах динамики.

1. Ряды динамики количественно характеризуют изменения изучаемых явлений во времени и состоят из двух элементов:

1. t - периоды либо моменты времени.

2. y - уровни ряда то есть непосредственно количественая характеристика изучаемых явлений.

в статистике рассматриваются следующие виды динамических рядов:

1. По методике построения ряды динамики подразделяются на интервальные и моментные. В Интервальных рядах уровни ряда получаются путём накопления сведений за определенный период времени, а в Моментных рядах уровни ряда фиксируются на определенный момент или дату.

2. По содержанию показателей ряды динамики могут состоять из абсолютных, относительных и средних величин.

3. В зависимости от величины интервалов ряды динамики могут быть как с равными, так и с неравными интервалами.

2. Для анализа рядов динамики применяется следующая система аналитических показателей:

1. Абсолютный прирос.

2. Темп роста.

3. Темп прироста.

4. Средние показатели:

• Средний уровень ряда.

• Средний абсолютный прирост.

• Средний темп роста.

• Средний темп прироста.

Все аналитические показатели кроме средних рассчитываются в двух формах, в Базисной и Цепной.

Базисные показатели определяются по сравнению с первоначальными то есть базисным уровнем ряда, а Цепные – по сравнению с предыдущим уровнем, для записи показателей применяются следующие обозначения:

Y1 – первоначальный (базисный) уровень ряда.

Yi – текущий уровень ряда то есть каждый, начиная со второго.

Yn – последний уровень ряда.

n – число уровней ряда, соответствующее числу моментов либо периодов времени.

1. Абсолютный прирост представляет собой разность между соответствующими уровнями ряда:

1. Базисный абсолютный прирост

2. Цепной абсолютный прирост

2. Темп Роста:

1. Базисный темп роста

2. Цепной темп роста

3. Темп прироста представляет собой относительную оценку изменения соответствующих абсолютных приростов уровней ряда и рассчитывается:

1. В базисной форме

2. Цепной темп прироста

Между темпами роста и темпами прироста существует следующая взаимосвязь.

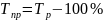
В табличной форме данные показатели можно представить следующим образом:

Показатель	Методы расчета
	цепные	базисные
1) Абсолютный прирост ( )
2) Коэффициент роста
3) Темп роста ( ), %
4) Темп прироста ( ), %
5) Абсолютное значение 1% прироста (А)

3. Если базисные и цепные показатели рассчитываются для каждого текущего уровня ряда, то средние показатели определяются в среднем за весь изучаемый период.

1. Средний абсолютный прирост показывает на сколько в среднем изменялись уровни ряда за изучаемый период в абсолютном выражении

2. Средний уровень ряда рассчитывается в зависимости от вида ряда динамики (моментный или интервальный) и величины интервалов в нем.

1. В интервальном ряду с равными интервалами средний уровень ряда определяется по средней арифметической простой

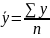
2. В моментных рядах динамики с равными интервалами средний уровень ряда рассчитывается по средней хронологической

3. В моментных и интервальных рядах с неравными интервалами средний уровень ряда определяется по средней арифметической взвешенной с учётом длительности каждого интервала

Средние показатели сведены в таблицу:

Показатель	Метод расчета
1) Средний уровень ( ): а) для интервального ряда с равными интервалами б) для моментного ряда с равными интервалами в) для интервального неравностоящего ряда (с неравными интервалами)
2) Средний абсолютный прирост (
3) Средний темп роста ( , %: а) с использованием уровней ряда б) с использованием последовательних цепных темпов роста, выраженных в коэффициентах
4) Средний темп прироста , %	=

Пример:

Для расчета процентных доходов по депозитам из лиц банком применялись в течении года следующие процентные вставки.

Месяц	Процентная ставка
Январь - Март Апрель – Май Июнь – Сентябрь Октябрь - Декабрь	12 11 9 13

Определить среднегодовую процентную ставку.

Ряд моментный с неравными интервалами

Пример:

Имеются следующие данные об остатках готовой продукции на складе производственного предприятия, миллионов рублей.

Дата	Готовая продукция
01.01 01.02 01.03 01.04	5.9 6.2 7.8 6.9

Определить средние остатки готовой продукции предприятия за первый квартал.

Ряд моментный с равными интервалами

3. Средний темп роста, определяется по средней геометрической

4. Средний темп прироста

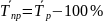
Пример:

Имеются данные об объеме отгруженных товаров организаций Свердловской обл. по виду экономической деятельности «Обрабатывающие производства».

Год	Объем отгруженных товаров, мрд .р.	Индекс цен производителей промышленных товаров, декабрь текущего к декабрю предыдущего, %
2005 2006 2007 2008 2009	470,7 602,5 746,1 823,5 647,8	111,9 109,2 112,8 114,8 103,8

Сделать выводы о реальной динамике объемов отгрузки, рассчитав все аналитические показатели (базисные, цепные и средние).
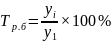
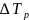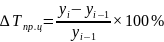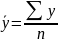
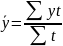
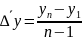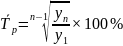