29.Свойства сходящихся числовых рядов.

Теорема 1(ассоциативное свойство)

Если ряд сходится, то ряд полученный с помощью произвольной группировки его слагаемых сходится к той же сумме.

Док-во

расставим скобки роизвольным образом.

-

…

По условию ряд сходится,а , значит, сходится последовательность кго частичных суммм . А последовательность является последовательностью , а , значит, сходиться к той же сумме, т .е. - сходиться.

30. Функциональные ряды: основные понятия.

Определение 1.

Пусть дана последовательность функций f₁(x), f₂(x), f₃(x)… Возьмем конкретное значение x=x_1. Пусть в этой точке все функции определены, поставим x₁ в каждую из них. Получим: f₁(x₁), f₂(x₁), f₃(x₁) … Получилась числовая последовательность. Если эта последовательность сходится, то говорят, что функциональная последовательность сходится в точке x_1.

Определение 2.

Пусть дана функциональная последовательность f₁(x₁), f₂(x₁), f₃(x₁) … Множество всех значений х, в которых последовательность сходится, называется областью сходимости функциональной последовательности.

Определение 3.

Пусть Х - область сходимости функциональной последовательности {f_n(x)}. Возьмем конкретное число х є Х и рассмотрим числовую последовательность f₁(x), f₂(x), f₃(x)…, она сходится, но ее предел зависит от х. Обозначим его f(x). Тем самым, на множестве Х определим функцию f(x). Эта функция называется предельной для функциональной последовательности. .

Определение 4.

Функциональным рядом называется бесконечная сумма функций u₁(x)+u₂(x)+u₃(x)+…= .

Частичной суммой функционального ряда называется S_n (x)= u₁(x)+u₂(x)+u₃(x)+…+ u_n(x)

S₁(x)= u₁(x)

S₂ (x)= u₁(x)+u₂(x)

S₃ (x)= u₁(x)+u₂(x)+u₃(x)

………..

Таким образом, получилась функциональная последовательность S₁(x), S₂(x), S₃(x), …

Область сходимости этой функциональной последовательности, называется областью сходимости функционального ряда, а предельная функция для этой последовательности называется суммой ряда. ( ).

31. Равномерная сходимость функциональных рядов.

Определение 1.

Пусть дан функциональный ряд и пусть существует числовой знакоположительный сходящийся ряд такой, что на всей области сходимости функционального ряда выполнено:| |≤ Ɐ . Тогда данный функциональный ряд называется равномерно сходящимся, а ряд называют мажорантой функционального ряда.

Замечание 1.

Если ряд сходится на множестве Х, то он сходится и в обычном смысле ⱯхєХ. Для конкретных х є Х соответственно, числовой ряд будет сходиться абсолютно.

Равномерно сходящиеся ряды обладают следующими свойствами.

Теорема 1.

Если состоит из непрерывных функций и равномерно сходится к сумме на множестве Х, то – непрерывная функция на множестве Х.

Это распространение известного свойства, о сумме непрерывных функций, на случай бесконечного кол-ва слагаемых.

Теорема 2.

Пусть состоит из интегрируемых на отрезке [а,b] функций и равномерно сходится на этом отрезке функции , тогда ряд можно почленно интегрировать.

Это распространение на бесконечные суммы известного свойства: интеграл суммы = сумме интегралов.

Важный пример.

Рассмотрим ряд, состоящий из членов геометрической прогрессии: 1-х²+х⁴-х⁶+…

b₁ = 1, q = -х²

|q |< 1 => |х|< 1

Для |х|< 1 можно доказать, что ряд сходится равномерно.

По Теореме 2 проинтегрируем ряд по отрезку [0,x]:

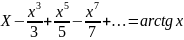
Слева получился ряд с областью сходимости [-1,1]. Можно доказать с помощью подстановки.

Замечание 2.

Полученный ряд используется для отыскания конкретных значений арктангенса и знаков числа П.

Подставим вместо х единицу.

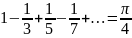
Теорема 3.

Пусть ряд сходится к сумме на множестве Х, а ряд, составленный из производных ( ), равномерно сходится на этом же множестве к сумме Q(x)=> Sˈ(x)= Q(x) (производная суммы = сумме производных)