25. Признак Даламбера. Радикальный признак Коши.

Теорема. Признак Даламбера.

Пусть для существует , тогда:

1. Если D<1, то ряд сходится

2. Если D>1, то ряд расходится

Теорема. Радикальный признак Коши.

Пусть для знакоположительного ряда тогда:

1. k<1=> Ряд сходится

2. k>1 => Ряд расходится

3. k=1 => ответа на вопрос нет.

Доказательство:

Распишем определение предела: ( )(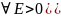

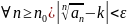
Распишем последнее неравенство:

Рассмотрим первый случай, где k<1: подберем так, чтобы . Тогда из правой части неравенства (*) следует

;

Т.к q<1, то сходится, но тогда по первой теореме сравнения сходится и ряд . Второй случай доказывается аналогично по левой части неравенства (*)

26. Интегральный признак Коши.

Теорема.

Пусть для знакоположительного ряда поставлена в соответствие функция y=f(x), обладающая следующими свойствами:

1. Определена непрерывно, убывает на

2. f(n) =

, ряд сходится  сходится несобственный интеграл

Доказательство:

Идея доказательства:

Площадь вписанной ступенчатой фигуры = нижней сумме Дарбу для такого способа разбиения луча

Площадь красных квадратов – разность между верхней и нижней суммой Дарбу

Площадь описанной ступенчатой фигуры = верхней сумме Дарбу

Нижняя сумма Дарбу < верхняя сумма Дарбу

Каждый столб имеет ширину = 1, а высота описанного столба = членам ряда. Значит верхняя сумма Дарбу = S ряда, нижняя сумма Дарбу = S Ряда без a₁

«=>» Если сходится ряд, верхняя сумма Дарбу которого является конечным числом, то сходится и интеграл, т.к он еще меньше чем верхняя сумма Дарбу.

«<=» Если сходится интеграл, то есть он равен конечному числу, то нижняя сумма Дарбу еще меньше, а она равна сумме ряда без a₁ => сумма ряда – конечное число.

27. Признак Лейбница

Теорема (Признак Лейбница)

Пусть дан знакочередующийся ряд ,причем >0, монотонно убывая, тогда ряд сходится.

0

Доказательство:

S1=

S2=

S3= , S2 S4 S3 S1

S4= ,

…………………………………..

Получилась последовательность вложенных отрезков: [S2;S3]Ↄ[S4;S3] Ↄ[S6;S5] …..

Для любой последовательности вложенных отрезков есть хотя бы одна общая точка. Длина отрезка = .

Последовательность{ } является последовательностью{ }. А если последовательность сходится, то и любая ее последовательность сходится к тому же пределу. Следовательно, .

Получилось, что длины выложенных отрезков стремятся к нулю, т.е. отрезки являются стягивающимися, а значит, они имеют единственную общую точку, она и будет суммой ряда.

Пример:

1- + - +…

= 0, монотонна убывая и из этого следует, что ряд сходится. Этот ряд называется рядом Лейбница.

28. Абсолютная и условная сходимость.

Определение1 – пусть даны знакопеременный ряд и пусть известно, что ряд сходиться. Тогда говорят, что ряд сходится абсолютно.

Теорема 2(теорема Коши) Всякий абсолютно сходящийся ряд сходится в обычном смысле.

Замечание – обратное не верно, т.е. из обычной сходимости не следует абсолютная сходимость.

Пример - ряд Лейбница 1- + - +… сходится, а соответствующий ряд из модулей 1+ + + + является гармоническим и расходиться.

Определение 2 – Если ряд сходится, а ряд расходиться, то говорят, что ряд сходиться неабсолютно или условно.

Пример- ряд Лейбница сходиться условно.

Расход. сход.

Абсол. Сходим.

Услов. Сход.