
- •1. Первообразная и неопределенный интеграл, их свойства.
- •2. Таблица основных неопределенных интегралов.
- •2 Случай
- •3. Вычисление неопределенных интегралов: методы подстановки и замены переменной.
- •4. Метод интегрирования по частям.
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций.
- •8. Суммы Дарбу. Определенный интеграл.
- •9.Свойства определенного интеграла: свойство аддитивности, теорема о среднем.
- •10. Существование первообразной у непрерывной функции.
- •11. Формула Ньютона-Лейбница.
- •12. Свойства определенного интеграла
- •13. Вычисление площадей плоских фигур с помощью определенного интеграла в случае явного задания функции.
- •1 4. Вычисление площадей плоских фигур с помощью определенного интеграла в случае параметрического задания функции. Площадь эллипса.
- •15. Вычисление площадей плоских фигур в полярной системе координат.
- •16. Вычисление длин дуг
- •17. Вычисление объемов тел. Объем тела вращения.
- •18. Несобственные интегралы 1-го рода
- •Важный интеграл.
- •19. Несобственные интегралы второго рода
- •20. Числовые ряды: основные понятия
- •21. Исследование произвольных числовых рядов на сходимость.
- •22. Исследование на сходимость знакоположительных рядов.
- •23. Первая теорема сравнения.
- •24. Вторая теорема сравнения.
- •25. Признак Даламбера. Радикальный признак Коши.
- •26. Интегральный признак Коши.
- •27. Признак Лейбница
- •28. Абсолютная и условная сходимость.
- •29.Свойства сходящихся числовых рядов.
- •30. Функциональные ряды: основные понятия.
- •31. Равномерная сходимость функциональных рядов.
- •32. Степенные ряды
- •33. Ряды Тейлора и Маклорена.
- •38. Разложение в ряд Маклорена функции .
Важный интеграл.
Исследуем
на сходимость
 ,
где r
,
где r
 R
R
1й случай r = 1 => интеграл расходится
2й случай r ≠ 1
 =
= =
=

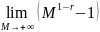 =
(=*)
=
(=*)
(=*) = +∞
= +∞
Следовательно, интеграл расходится
б)


(=*)
Следовательно, интеграл сходится
Вывод:
Интеграл
расходится при
 , сходится при
, сходится при
На несобственные интегралы 1-го рода можно распространить формулу Ньютона – Лейбница
=

19. Несобственные интегралы второго рода
 Попробуем
найти S фигуры ограниченной осями
координат, прямой x=4 и графиком функции
y=1/x
Попробуем
найти S фигуры ограниченной осями
координат, прямой x=4 и графиком функции
y=1/x 
c
Sкр тр=
S=
Определение 1.
Пусть
функция y=f(x)определена на полуинтервале
(a, b] и при этом
 Этот предел называют несобственным
интегралом второго рода. И обозначают
Этот предел называют несобственным
интегралом второго рода. И обозначают

Если это
предел равен конечному числу, то говорят,
что Несобственный интеграл второго
рода сходится, а если предел не существует
или равен
 ,
то расходится.
,
то расходится.
В нашем
примере S можно было вычислить как S= т к с- особая точка,
т к с- особая точка,
 .
.
Та точка, в которой функция явл-ся б/б по отношению к несобственному интегралу называется особой точкой. В роли особой точки может выступать не только нижний предел интегрирования, но и верхний
Определение 2
 Пусть
функция y=f(x)определена на полуинтервале
[a, b) и при этом
Пусть
функция y=f(x)определена на полуинтервале
[a, b) и при этом
 Рассмотрим предел
Рассмотрим предел
 Этот предел называют несобственным
интегралом второго рода. И обозначают
Этот предел называют несобственным
интегралом второго рода. И обозначают
Определение 3

Пусть функция y=f(x)определена на [a, c) U
(c, b] и gecnm
 Рассмотрим предел
Рассмотрим предел
 . Этот предел называют несобственным
интегралом второго рода. И обозначают
. Этот предел называют несобственным
интегралом второго рода. И обозначают
Пример
-1 0 1
 На отрезке [a,b] есть особая точка О, а
значит это несобств. интеграл 2-го рода.
На отрезке [a,b] есть особая точка О, а
значит это несобств. интеграл 2-го рода.

Для несобственных интегралов 2 – го рода иногда удается использовать ф-лу Н-Л
Пусть задан несобств. интеграл на [a,b] и с – особая точка a<c<b

Потребуем,
чтобы предел был равен нулю, Для этого
нужно чтобы
 ,
а это значит, что первообразная F(x) должна
быть непрерывна в точке с. Таким образом
доказана следующая теорема.
,
а это значит, что первообразная F(x) должна
быть непрерывна в точке с. Таким образом
доказана следующая теорема.
Теорема.
Пусть для функции y=f(x) рассматриваемой на отрезке [a,b], с – особая точка a<c<b и пусть первообразная этой функции непрерывна в точке с, тогда для вычисления несобственного интеграла 2-го рода можно применить формулу Н-Л
Пример
 В точке с F(x) непрерывна
В точке с F(x) непрерывна

20. Числовые ряды: основные понятия
Определение 1
Числовым
рядом называется бесконечная сумма
вида а1+ а2+ а3+… , (
( )
)
Определение 2
Частичной
суммой ряда
называется сумма а1+ а2+ а3+…+ ,
обозначается Sn. Ряд без частичной суммы
называется Остатком ряда (Rn): (а1+ а2+
а3+…+
+
аn+1+ аn+2+… )=(Sn+ Rn) Остаток ряда тоже является
рядом
,
обозначается Sn. Ряд без частичной суммы
называется Остатком ряда (Rn): (а1+ а2+
а3+…+
+
аn+1+ аn+2+… )=(Sn+ Rn) Остаток ряда тоже является
рядом
Определение 3
Если
существует и равен конечному числу
предел Частичной суммы ( )
то ряд называется сходящимся, а этот
предел называется суммой ряда (S) (
)
то ряд называется сходящимся, а этот
предел называется суммой ряда (S) ( )
)
Пример 1
 – сумма геометрической прогрессии у
которой
– сумма геометрической прогрессии у
которой



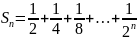


Тот де
результат можно было получить по
известной из школы формуле суммы беск-но
убывающей геометрической прогрессии
:

Пример 2 (в общем виде)
 Рассмотрим 4 случая:
Рассмотрим 4 случая:

 – ряд сходится
– ряд сходится ряд 1+1+1+1… - ряд расходится
ряд 1+1+1+1… - ряд расходится

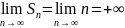
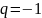
 – не существует т. е. расходится
– не существует т. е. расходится

 ряд расходится
ряд расходится
Вывод: Ряд

Пример 3


 -
ряд сходится
-
ряд сходится
Пример 4 ( гармонический ряд)
 Выпишем частичную сумму на слагаемые
Выпишем частичную сумму на слагаемые


Во всех скобках заменим каждое слагаемое на последнее в этой скобке. От этого сумма уменьшится


При
 последовательность
последовательность
 неограниченно возрастает, а частичная
сумма принимает еще большее значение
поэтому последовательность частичных
сумм
неограниченно возрастает, а частичная
сумма принимает еще большее значение
поэтому последовательность частичных
сумм
 ,
то есть гармонический ряд расходится
,
то есть гармонический ряд расходится

