15. Вычисление площадей плоских фигур в полярной системе координат.

Построим в полярной системе координат аналог криволинейной трапеции. Уравнение будет задавать луч выходящий из полюса.

Для отыскания площади строятся множества верхних и нижних сумм Дорбу, если от функции построить непрерывность, то она будет интегрируема и построенные множества будут разделяться единственным числом:

16. Вычисление длин дуг

1)

2)

Зададим ту же функцию параметрически

a ≤ t ≤ b

= = =

3)

Зададим ту же функцию параметрически:

p = p(φ)

Воспользуемся случаем номер 1

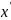= cosφ + p = cosφ – psinφ

= sinφ + p = sinφ + pcosφ

+ = φ =

17. Вычисление объемов тел. Объем тела вращения.

Ц илиндрическое тело

Тело, состоящее из нескольких цилиндрических тел без общих внутренних точек, называется кусочно-цилиндрическим.

Рассмотрим теперь тело, устроенное следующим образом:

1) Оно полностью заключено внутри полосы, образованной двумя плоскостями α и β, параллельными некоторой фиксированной плоскости γ

2 ) Построим все возможные сечения этого тела, плоскостями параллельными γ. Пусть площадь каждого сечения можно задать функцией S(x), где S – это расстояние от плоскости сечения до плоскости γ.

3) S(x) непрерывная функция на отрезке , где a и b – это расстояния от плоскости γ до плоскостей α и β.

Такое тело называется регулярным.

Теорема

Объем регулярного тела вычисляется по формуле

Док-во:

В качестве плоскости γ выберем плоскость Z . Осуществим разбиение Т отрезка от а до в на ряд мелких участков:

Через каждую точку разбиения проведем плоскость параллельную γ, тогда данное тело разрежется на ряд узких ломтиков. Рассмотрим отдельно ломтик № К. Для него х . Обозначим длину этого отрезка . Так как по условию тело регулярное, то функция S(x) непрерывная, следовательно, на этом отрезке она достигает наименьшего и наибольшего значения. Обозначим: – наименьшее значение S(x)

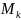- наибольшее значение S(x). Построим два цилиндрических тела, у которых в основании будут сечения с площадью и , а высота . Одно из них будет полностью внутри ломтика, а другое будет содержать ломтик внутри себя.

=

Сделаем тоже самое по всем ломтикам. В итоге построим внутреннее кусочно-цилиндрическое тело и внешнее. Тогда:

– это верхняя сумма Дарбу для функции f(x)

- это нижняя сумма Дарбу для функции f(x).

Проведем теперь все возможные разбиения и для каждого из них составим внутреннюю и внешнюю сумму Дарбу. Все верхние суммы Дарбу объединим в одно множество, все нижние в другое. Так как тело по условию регулярное, то функция S(x) непрерывна, а значит интегрируема, следовательно, множество верхних и нижних сумм Дарбу разделяются единственным числом, и оно равно:

.

18. Несобственные интегралы 1-го рода

Рассмотрим функцию

Попробуем найти площадь фигуры, ограниченной графиком этой функции и осью OX.

Найдем площадь правой половины.

M

Введем ограничение x ≤ M, вычислим площадь криволинейной трапеции.

0

S_{крив.трап.} = = arctg x = arctg M

Для нахождения площади бесконечной фигуры, устреми М → +∞

S_1/2 =

S = π

После рассмотренного примера, можно предположить, что у любой бесконечной фигуры, можно найти площадь, если график асимптотически приближается к оси x.

M

1

Пример

M

1

S_{крив.трап.} = = = - =

S

Определение 1.

Пусть функция y = f (x) определена на луче и интегрируема на любом отрезке . Если существует , то он называется несобственным интегралом 1-го рода, и обозначается:

Замечание

Если этот предел не существует или равен бесконечности, можно использовать то же самое обозначение, но в этом случае говорят, чтонесобственный интеграл расходится. А если предел равен конечному числу – интеграл сходится.

Таким образом - расходится,

а если смотерть - сходится.

Всего существует несобственных интегралов 1-го рода 3 вида:

• 1 вид:

• 2 вид:

• 3 вид: