10. Существование первообразной у непрерывной функции.

Теорема.

Если функция y=f(x) непрерывна на отрезке [a;b], то функция Ф(х)= дифференцируема в любой точке этого отрезка, причём Ф’(x)=f(x). Иными словами интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции.

Доказательство:

Дадим переменной х приращение Δх так, чтобы x+Δx∈[a;b] и вычислим Ф’(x)

Ф(x+Δx)=

• 

• 

= f(x)

Эта теорема означает, что если функция y=f(x) непрерывна на отрезке [a;b], то она имеет на этом отрезке первообразную, например, функцию Ф(х).

11. Формула Ньютона-Лейбница.

Теорема. (Формула Ньютона-Лейбница)

Если функция y=f(x) непрерывна на отрезке [a;b], то .

Доказательство:

1. Функция непрерывна на [a;b], следовательно, она интегрируема (см.Т.1 (Любая непрерывная на отрезке функция интегрируема на нём))

2. Функция непрерывна на [a;b], следовательно, у неё существует первообразная, например,

Для другой любой первообразной Ф(х): Ф(х)=F(х)+с

3. 

Это равенство записано для функции, у которой независимая переменная t.

- формула Ньютона-Лейбница.

Пример.

12. Свойства определенного интеграла

1. Доказательство: Вычислим левую/правую часть по формуле Ньютона-Лейбница G(x) – первообразная для g(x) F(x) – первообразная для f(x)

2. Доказательство: Продифференцируем левую и правую части равенства. Получим: В левой части получим: В правой части по правилам дифференцирования получим: Пример: Можно было не разбивать один интеграл на три, а воспользоваться свойствами первообразной.

3. Если f(x)≥0 для любого х на отрезке [а,b], то 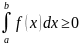Доказательство: f(x)≥0 для любого ТS≥0 Геометрический смысл заключается в том, что если график функции выше оси Ох, то интеграл принимает положительные значения и совпадает с площадью криволинейной трапеции.

4. Если f(x)≤g(x) для любого х на отрезке [а,b], то Доказательство: f(x)≤g(x); g(x)-f(x)≥0. По свойству 3: По свойствам 1 и 2 левую часть представим Геометрическое истолкование: Площадь криволинейной трапеции получится под тем графиком, который выше.

13. Вычисление площадей плоских фигур с помощью определенного интеграла в случае явного задания функции.

С помощью определенного интеграла можно вычислять площади различных плоских фигур, в том числе, не являющихся криволинейными трапециями.

О существим параллельный перенос графиков обеих функций так, чтобы вся фигуры была выше оси x. При переносе на одно и то же расстояние площадь не изменится.

П ример 1. Найти площадь фигуры, ограниченной линиями:

; ; ; При

Пример 2. Вычислите интеграл:

1 4. Вычисление площадей плоских фигур с помощью определенного интеграла в случае параметрического задания функции. Площадь эллипса.

Пусть задана параметрически:

Чтобы определенный интеграл задать через параметр t, нужно по знаком интеграла перейти к новой переменной. Символ dx теперь означает дифференциал функции .

Для того, чтобы и находились единственным образом, следует потребовать, чтобы функция была обратима, для этого достаточно монотонности.

Пример. Вычислить площадь эллипса:

Окружность является частным случаем эллипса с полуосями равными R, .
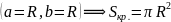