1. Первообразная и неопределенный интеграл, их свойства.
Определение
1.
Функция
называется первообразной для функции
на X,
если
.
Свойства
первообразных:
1)
Первообразные суммы равны сумме
первообразных
2) Постоянный множитель
можно выносить за знак первообразной.
3)
Если
– первообразная для
,
то
– первообразная для
a
Доказательство:
Теорема.
Если
функция
имеет первообразную
,
то она имеет бесконечно много первообразных
и все они описываются формулой
Практически это означает, что все первообразные одной функции отличаются друг от друга на константу.
Доказательство:
– первообразные для функции
Введем в рассмотрение вспомогательную
функцию, равную разности первообразных
.
Нам
достаточно показать, что
– постоянная функция.
По
условию постоянства функций
– константа.
Определение
2.
Множество
всех первообразных
называется неопределенным интегралом,
и обозначается:
Свойства
неопределенных интегралов:
1)
2)
3)
2. Таблица основных неопределенных интегралов.
1)
2)
3)
,
если
.
Доказательство:
4)
Доказательство:
1
случай
2 Случай
5)
6)
7)
8)
9)
10)
11)
Доказательство:
12)
13)
3. Вычисление неопределенных интегралов: методы подстановки и замены переменной.
I. Метод подстановки – этот метод основан на инвариантности формы первого дифференциала.
y= f(x)
dy
=
dx
Пусть F(x) – первообразная f(x)
dF(x)
=
dx
dF(x) = f(x)dx
Эта формула сохраняет силу как в случаи, когда x независимая переменная, так и в случаи, когда x сам является функцией.
Проинтегрируем обе части этого равенства:
Эта известная формула, но теперь мы выясним, то она сохраняет силу и для случая, когда x зависимая переменная x = x(t).
Для практики это означает, что вместе x мы имеем право подстановки любую функцию от t, если в этом есть смысл.
Пример 1.
Для того, чтобы все x из области определения были исчерпаны достаточно рассмотреть t>0
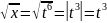
Пример 2.
На практике гораздо чаще этот метод применяется в обратную сторону:
Метод
замены переменной
– какое – то большое выражение заменят
новой переменной t
и вычисляют интегралы как-будто t
независимая переменная.
Пример 3.
Для применения этого метода под знаком интеграла должна содержаться некоторая функция и дифференциал от нее т.к. части подынтегрального выражения, должны быть связать через производную.
4. Метод интегрирования по частям.
Этот метод применяют тогда, когда под знаком интеграла содержатся функции разных классов.
Пусть функции U и V - дифференцируемы, тогда можем вычислить:
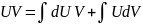
При выборе множителей U и dV:
За U стараются принять функцию, производная от которой проще самой функции. (Н-р,
,
lnx,
arc…,
и тд)За dV принимают выражение, которое легко интегрируется.
5. Интегрирование рациональных функций.
Рациональной
называется функция вида
, где p
и q
– многочлены.
Нам понадобятся некоторые сведения из алгебры: 1) называется правильной если степень числителя меньше степени знаменателя и неправильной если наоборот.
2) Из неправильной дроби всегда можно выделить целую часть (деление многочленов столбиком)
3) Два многочлена называется тождественно равными <=> равны их коэффициенты при одинаковых степенях.
4) многочлен можно разложить на множители 1ой и 2ой степени
D>0 ax2+bx+c=a(x-x1) (x-x2)
D=0 => полный квадрат
Не раскладываются на множители только линейные многочлены и квадраты с отрицательным D.
5) простую дробь можно представить в виде суммы следующих типов дробей:
1)
;
2)
;
3)
(для D<0);
4)
(для D<0)
Алгоритм
вычисления
1) Если дробь неправильная, то выделить из нее целую часть (деление в столбик)
2) В получившейся правой части разложить знаменатель на множители
3) Представить правую часть в виде суммы дробей указанных 4х типов:
а) (х-а)
б)
(х-а)n
в) (x2+px+q)
г)
(x2+px+q)n
4) Выделить интеграл как сумму интегралов получившихся выражений
Рекуррентная формула
In=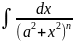
In+1=
In
+
*
