МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД

ГАЙВОРОНСЬКИЙ ПОЛІТЕХНІЧНИЙ КОЛЕДЖ

Завдання

для державної підсумкової атестації

з математики

Розробив викладач Костенко А. Л.

Розглянуто на засіданні циклової комісії загальноосвітніх дисциплін

Протокол №_ від «__» ________20__ р. Голова комісії ________ (Лошакова Л.Я.)

Гайворон 2017 р.

Пояснювальна записка

Методична розробка «Завдання для державної підсумкової атестації з математики» призначена для проведення державної підсумкової атестації з математики для студентів II курсу коледжу. Вона містить 25 варіантів атестаційної роботи, кожний з яких складається із трьох частин. Ці частини відрізняються за формою тестових завдань і за рівнем їх складності. Зміст усіх навчальних завдань відповідає чинним програмам з математики для академічного рівня.

Завдання атестаційної роботи студенти виконують на аркушах зі штампом навчального закладу. Державна підсумкова атестація з математики проводиться протягом 135 хв.

У першій частині атестаційної роботи пропонується 15 завдань з вибором однієї правильної відповіді. До кожного завдання наведено чотири варіанти відповіді, з яких тільки одна є правильною. Завдання з вибором однієї відповіді вважається виконаним правильно, якщо в аркуші для відповідей вказано тільки одну літеру – ту, якою позначено правильну відповідь. При цьому студент не повинен наводити будь-які міркування, що пояснюють його вибір.

Кожне правильно розв’язане завдання першої частини оцінюється одним балом. Якщо в аркуші для відповідей вказано правильну відповідь, то за виконання цього завдання нараховується 1 бал. Якщо ж вказана студентом відповідь є неправильною, то виконання завдання оцінюється в 0 балів.

Друга частина атестаційної роботи складається із 6 завдань відкритої форми з короткою відповіддю. Завдання цієї частини вважається виконаним правильно, якщо в аркуші для відповідей записано тільки правильну відповідь (наприклад число, вираз, корені рівняння тощо). Усі необхідні обчислення, перетворення, побудови тощо студенти виконують на чернетках.

Правильне розв’язання кожного із завдань другої частини оцінюється двома балами: якщо в аркуші для відповідей вказано правильну відповідь до завдання, то за це нараховується 2 бали, якщо ж указана студентом відповідь є неправильною, то бали за таке завдання не нараховуються. Часткове виконання завдання другої частини (наприклад, якщо студент правильно знайшов один із коренів рівняння) оцінюється 1 балом.

Третя частина атестаційної роботи складається із трьох завдань відкритої форми з розгорнутою відповіддю. Такі завдання вважаються виконаними правильно, якщо студент навів розгорнутий запис розв’язування з обґрунтуванням кожного його етапу та дав правильну відповідь.

Правильне розв’язання завдань третьої частини оцінюється п’ятьма балами. Якщо студент отримав правильну відповідь і навів повне її обґрунтування, то за це нараховується 5 балів. Якщо студент отримав правильну відповідь, записав правильний хід розв’язування, але в процесі розв’язування допустив помилку обчислювального або логічного (при обґрунтуванні) характеру, то за це нараховується 4 бали. У випадку, якщо студент суттєво наблизився до правильного кінцевого результату або знайшов лише частину правильної відповіді, то він одержує 3 бали. Якщо студент розпочав розв’язувати завдання правильно, але в процесі розв’язування припустився помилки в застосуванні необхідного твердження чи формули, то за це нараховується 2 бали. Якщо ж студент лише розпочав правильно розв’язувати завдання або розпочав хибним шляхом, але в подальшому окремі етапи розв’язування виконав правильно, то він одержує 1 бал. Розв’язання, яке не відповідає жодному з наведених вище критеріїв, оцінюється в 0 балів.

Виправлення і закреслення в оформленні розв’язання завдань третьої частини, якщо вони зроблені акуратно, не є підставою для зниження оцінки.

Сума балів, нарахованих за виконані студентом завдання, переводиться в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів. Максимально можлива сума балів за атестаційну роботу становить 42. Відповідність кількості набраних студентом балів оцінці за 12-бальною системою оцінювання навчальних досягнень студентів наведено в таблиці.

Кількість набраних балів	0-3	4-6	7-8	9-11	12-13	14-15	16-19	20-23	24-27	28-32	33-37	38-42
Оцінка за 12-бальною системою	1	2	3	4	5	6	7	8	9	10	11	12

Варіант 1

Частина перша

1. Обчисліть .

А) 199; Б) 3; В) 17; Г) 44.

2. Знайдіть розв’язок системи

А) ; Б) ; В) ; Г) .

3. Спростіть .

А) ; Б) ; В) ; Г) .

4. - арифметична прогресія, . Знайдіть .

А) 17; Б) -17; В) -19; Г) -15.

5. Обчисліть .

А) 9; Б) 6; В) 3; Г) інша відповідь.

6. Для функції знайдіть .

А) 0; Б) ; В) ; Г) 1.

7. Знайдіть похідну функції .

А) ; Б) ; В) ; Г) _.

8. Яка із вказаних функцій є показниковою?

А) ; Б) ; В) ; Г) .

9. Який із проміжків є областю визначення функції ?

А) ; Б) ; В) ; Г) .

10. Знайдіть площу фігури, обмежену лініями .

А) ; Б) ; В) ; Г) .

11. Точка належить відрізку см, см. Знайдіть довжину відрізка .

А) 10 см; Б) 6 см; В) 4 см; Г) 2 см.

12. Обчисліть суму внутрішніх кутів опуклого десятикутника.

А) ; Б) ; В) ; Г) .

13. Знайдіть суму векторів і .

А) ; Б) ; В) ; Г) .

14. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює 3 см, а висота – 7 см.

А) 84 см³; Б) 21 см³; В) 189 см³; Г) 63 см³.

15. Пряма паралельна площині , а пряма належить площині . Як можуть бути розташовані прямі і ? Виберіть правильне твердження.

А) Прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинатися;

Б) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинатися;

В) прямі і можуть перетинатися, не можуть бути паралельними або мимобіжними;

Г) прямі і можуть бути паралельними або мимобіжними, не можуть перетинатися.

Частина друга

16. Обчисліть значення виразу .

17. Розв’яжіть рівняння .

18. У коробці знаходиться 30 карток, що пронумеровані натуральними числами від 1 до 30. З коробки навмання взяли одну картку. Яка ймовірність того, що на ній записане число, яке не є дільником 30?

19. Знайдіть границю функції .

20. Хорда, довжина якої см, стягує дугу кола, градусна міра якої . Знайдіть довжину кола.

21. В основі прямої призми лежить рівнобедрений трикутник з кутом при вершині. Діагональ грані, що містить бічну сторону трикутника, дорівнює 6 см і утворює з площиною основи кут . Знайдіть об’єм призми.

Частина третя

22. Розв’яжіть рівняння .

23. Ділянку прямокутної форми потрібно з усіх сторін обгородити парканом завдовжки 200 м. Якими мають бути розміри цієї ділянки, щоб її площа була найбільшою?

24. Висота конуса дорівнює 4 см. Площа перерізу конуса площиною, що паралельна його основі, дорівнює половині площі основи. Знайдіть відстань від вершини конуса до перерізу.

Варіант 2

Частина перша

1. У процесі перегонки нафти утворюється 30% гасу. Скільки гасу утвориться після перегонки 240 т нафти?

А) 8 т; Б) 72 т; В) 800 т; Г) 24 т.

2. Винесіть за дужки спільний множник у виразі .

А) ; Б) ; В) ; Г) .

3. Обчисліть .

А) 1,5; Б) 1,1; В) 0,1; Г) -0,2.

4. Відомо, що . Яке з наведених чисел задовольняє цю умову?

А) 20,2; Б) 17,49; В) 20,01; Г) 18,49.

5. Чому дорівнює дискримінант квадратного рівняння ?

А) -8; Б) 16; В) 14; Г) -10.

6. Знайдіть область визначення функції .

А) ; Б) ; В) ; Г) .

7. На якому з рисунків зображено графік функції ?

8. Дано 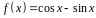. Знайдіть .

А) -1; Б) 0; В) 1; Г) 2.

9. Розв’яжіть рівняння .

А) ; В) ;

Б) ; Г) .

10. Стрілець у п’яти серіях з десяти пострілів у кожній влучив у мішень таку кількість разів: 8; 7; 9; 6; 7. Знайдіть розмах цієї вибірки.

А) 3; Б) 4; В) 7; Г) 9.

11. Бічна сторона рівнобедреного трикутника дорівнює 8 см, а кут при основі . Знайдіть площу трикутника.

А) 8 см²; Б) 16 см²; В) 32 см²; Г) см².

12. Яка точка симетрична точці відносно початку координат?

А) (1;-2;-4); Б) (-1;-2;4); В) (2;-1;4); Г) (1;2;-4).

13. Сторона основи правильної чотирикутної піраміди дорівнює 3 см, а апофема – 5 см. Знайдіть площу бічної поверхні піраміди.

А) 30 см²; Б) 15 см²; В) 60 см²; Г) 45 см².

14. Пряма перпендикулярна до площини , а пряма перетинає площину , але не є перпендикулярною до неї. Як можуть бути розташовані прямі і ? Виберіть правильне твердження.

А) Прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинатися;

Б) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинатися;

В) прямі і можуть перетинатися, не можуть бути паралельними або мимобіжними;

Г) прямі і можуть перетинатися або можуть бути мимобіжними, не можуть бути паралельними.

15. Площа основи конуса 12 см, висота конуса – 5 см. Чому дорівнює об’єм конуса?

А) 60 см³; Б) 20 см³; В) 30 см³; Г) 120 см³.