Задача-эталон 1
Коэффициент корреляции Спирмена (ρ или rs)
Требуется определить размер связи между уровнем концентрации фтора в питьевой воде и числом лиц, пораженных флюорозом (в процентах к числу обследованных) (табл. 2).
Таблица 2
Распространенность флюороза среди населения, употребляющего воду
с различным содержанием фтора
Содержание фтора в воде, мг/л |
Процент пораженных флюорозом |
Порядковый номер (ранг) |
Разность рангов |
Квадрат разности рангов |
|||
х |
у |
х1 |
у1 |
d (х1-у1) |
d2 |
||
Низкое 0,5 |
0,0 |
1 |
1 |
0 |
0,0 |
||
Оптимальное 1,0 |
3,0 |
2 |
2 |
0 |
0,0 |
||
Условно-допустимое 1,5 |
15,0 |
3 |
3 |
0 |
0,0 |
||
Повышенное 3,5 |
98,0 |
4 |
4,5 |
-0,5 |
0,25 |
||
Недопустимое 5,0 |
98,0 |
5 |
4,5 |
+0,5 |
0,25 |
||
|
|
|
|
|
d2=0,5 |
||
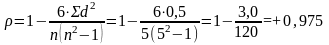(связь
сильная и прямая);
,
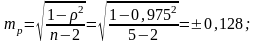
что соответствует вероятности
достоверности более 99%
Вывод: между уровнем концентрации фтора в питьевой воде и числом лиц, пораженных флюорозом, наблюдается статистически значимая прямая и сильная связь, так как коэффициент ранговой корреляции составил ρ= +0,975, уровень значимости р<0,01. Таким образом, с увеличением содержания фтора в воде увеличивается распространенность флюороза среди населения.
Задача-эталон 2
Коэффициент корреляции Пирсона (rxy)
Требуется определить, имеется ли зависимость между температурой тела и частотой пульса (условные данные) (табл. 3).
Последовательность расчета:
1. Построить вариационные ряды из парных признаков х и у.
2. Определить их средние величины - Мx и М.
3. Найти d - отклонение каждой варианты от средней для ряда x(dx = x - Mx) и для ряда y(dy = y - Mу).
4. Полученные отклонения перемножить (dx*dy) и просуммировать (dx*dy).
5. Каждое отклонение возвести в квадрат и суммировать по ряду х - dx2 и по ряду у - dу2.
6. Определить произведение dx2 · dу2 и из произведения
Рассчитать rxy по формуле:
.
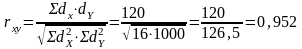Таблица 3
Зависимость между температурой тела и частотой сердечных сокращений
Температура тела, х |
Частота пульса в минуту, у |
dх |
dу |
dx*dy |
dх2 |
dу2 |
36 |
60 |
-2 |
-20 |
40 |
4 |
400 |
36 |
70 |
-2 |
-10 |
20 |
4 |
100 |
38 |
80 |
0 |
0 |
0 |
0 |
0 |
40 |
90 |
+2 |
+10 |
20 |
4 |
100 |
40 |
100 |
+2 |
+20 |
40 |
4 |
100 |
х Мх=38 |
у Му=80 |
dx |
dу |
dx·dу |
dx2 |
dу2 |
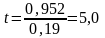что
соответствует вероятности достоверности
более 99%
Вывод: между температурой тела и частотой сердечных сокращений выявлена статистически значимая сильная прямая корреляционная связь, так как коэффициент корреляции составил r= +0,952, уровень значимости р<0,01. Таким образом, с увеличением температуры тела увеличивается частота сердечных сокращений.
Приложение1
Стандартные коэффициенты корреляции, которые считаются достоверными
(по Л.С. Каминскому)
Число степеней свободы n=n-2 |
Уровень вероятности p (в %) |
Число степеней свободы n=n-2 |
Уровень вероятности p (в %) |
||||
95,0 |
98,0 |
99,0 |
95,0 |
98,0 |
99,0 |
||
1 |
0,997 |
0,999 |
0,999 |
12 |
0,532 |
0,612 |
0,661 |
2 |
0,950 |
0,980 |
0,990 |
13 |
0,514 |
0,592 |
0,641 |
3 |
0,878 |
0,934 |
0,959 |
14 |
0,497 |
0,574 |
0,623 |
4 |
0,811 |
0,882 |
0,917 |
15 |
0,482 |
0,558 |
0,606 |
5 |
0,754 |
0,883 |
0,874 |
16 |
0,468 |
0,542 |
0,590 |
6 |
0,707 |
0,789 |
0,834 |
17 |
0,456 |
0,528 |
0,575 |
7 |
0,666 |
0,750 |
0,798 |
18 |
0,444 |
0,516 |
0,561 |
8 |
0,632 |
0,716 |
0,765 |
19 |
0,433 |
0,503 |
0,549 |
9 |
0,602 |
0,685 |
0,735 |
20 |
0,423 |
0,492 |
0,537 |
10 |
0,576 |
0,658 |
0,708 |
25 |
0,381 |
0,445 |
0,487 |
11 |
0,553 |
0,634 |
0,684 |
30 |
0,349 |
0,409 |
0,449 |
Подпись автора методической разработки_____________ Латыпов А.Б.
«30.06.2017г.»