
- •Механика грунтов в системе инженерных наук
- •Физическо-механические свойства грунтов
- •2.1. Составные элементы грунтов
- •2.2. Виды грунтов
- •2.3. Характеристики плотности, влажности и пористости грунта
- •Определение вида грунтов по их гранулометрическому составу и числу пластичности
- •2.5. Характеристики состояния грунтов по плотности сложения песков и консистенции глинистых грунтов
- •2.6. Сжимаемость грунтов и их сопротивление сдвигу
- •2.6.1. Сжимаемость грунтов
- •1.6.2. Сопротивление грунта сдвигу
- •2.7. Водопроницаемость грунтов. Закон ламинарной фильтрации
- •3. Основные закономерности механики грунтов на основе механики сплошных сред
- •3. 1. Распределение напряжений в массиве
- •3.2. Распределение контактных давлений под жестким фундаментом
- •3.3. Распределение давлений от собственного веса грунта
- •3.4. Расчет осадки сооружений
- •3.4.1. Расчет величины конечных осадок
- •3.3.2. Развитие осадки во времени
- •Значения степени уплотнения
- •3.3.3. Реология грунтов
- •4. Условия предельного равновесия и несущая способность грунтов
- •4.1. Понятие о фазах напряженного состояния грунта
- •4.1.1. Начальная критическая нагрузка на грунт
- •4.2. Предельная нагрузка для сыпучих и связных грунтов
- •5. Давление грунтов на ограждение
- •5.1. Давление грунтов на подпорную стенку
- •5.2. Приближенный метод кулона для определения активного и пассивного давления грунтов на подпорные стенки
- •6. Устойчивость откосов
- •6.1. Устойчивость откоса, сложенного сыпучими грунтами
- •6.2. Устойчивость откоса, сложенного связными грунтами
- •6.3. Устойчивость откоса, сложенного грунтами, обладающими трением и сцеплением
- •Приложения
- •Значения коэффициента к1 по формуле (3.11)
- •Значения коэффициента к2 в формуле (3.13)
- •Значения коэффициента к3 в формуле (3.14)
- •Значение коэффициента к4 в формуле (3.16)
- •Значения коэффициента к5 в формуле (3.18)
- •Значения коэффициента к6 в формуле (3.22)
- •Значения коэффициента к7 в формуле (3.23)
- •Значения коэффициента к8 (по м.И. Горбунову-Посадову), форм. (3.24)
- •Значение коэффициента к9 в формуле (3.25) (по к.Е. Егорову)
- •Значения коэффициента (по м.И. Горбунову-Посадову) для фундаментов различной формы (форм. 3.35)
- •Значения коэффициента в формуле (2.19) (по м.И. Горбунову-Посадову) для фундамента различной формы (форм. 3.35)
- •Значение безразмерной функции к в формуле (3.36) к.Е. Егорова для фундаментов различной формы
- •Значение коэффициента эквивалентного слоя (по н.А. Цытовичу) (форм. 3.38)
- •Значение n (форм. 3.50) для вычисления величины осадки грунта как функции времени
- •Значение коэффициентов а и в для определения коэффициента устойчивости откоса
- •Тесты для самоконтроля
- •Рекомендуемая литература
3. Основные закономерности механики грунтов на основе механики сплошных сред
3. 1. Распределение напряжений в массиве
Для вычисления напряжений в массиве грунта применяются уравнения теории упругости (линейно-деформируемого тела). Упругое тело характеризуется тем, что в нем упругие деформации линейно зависят от напряжений и отсутствуют остаточные (пластические) деформации. Для упругого тела справедлив закон Гука:
![]() (3.1)
(3.1)
где
![]() - относительные деформации;
- относительные деформации;
![]() -
модуль упругости.
-
модуль упругости.
Линейно-деформируемое тело формально подчиняется тоже закону Гука, однако, как указывалось во введении, вместо модуля упругости E в нем используется модуль общей деформации E0, который учитывает не только упругие, но и остаточные деформации, присущие реальному грунтовому основанию:
![]() . (3.2)
. (3.2)
Уравнения механики сплошных сред справедливы для всех случаев, когда: а) напряжения не вызывают появления в грунтах областей пластических деформаций, б) достигнута стабилизация напряжений и вызванных ими деформаций грунта.
В механике грунтов рассматриваются два случая распределения напряжений: 1) от нагрузок, передаваемых через гибкие фундаменты или насыпи; 2) от нагрузок, передаваемых через жесткие фундаменты.
Действие сосредоточенной силы (основная задача). При этом рассмотривается действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости (рис. 3.1). Полупространство считается однородным в глубину и в стороны и линейно деформируемым.
Задача заключается в определении всех составляющих напряжений σz, σy, σx, τzy, τzx, τxy, а также перемещений wz, wy, wx для любой точки полупространства, имеющей координаты z, x, y или R и β.
Поставленная
задача для упругого (следовательно, и
любого линейного деформируемого)
полупространства впервые была полностью
решена проф. Ж. Буссиненском (1885 г.), а
определение напряжений для площадок,
параллельных ограничивающей
полупространство плоскости – проф. В.
Кирпичевым и Н.А. Цытовичем (1923 –1934 гг.).
Здесь для примера приводится вывод
только формулы вертикальных сжимающих
напряжений σz
для площадок, параллельных ограничивающей
плоскости, как наиболее часто используемых
в расчетной практике. Вывод формул для
остальных составляющих напряжений
![]()
![]() τzx,
и τzx
можно найти в специальной литературе.
τzx,
и τzx
можно найти в специальной литературе.
Для точки М (рис. 3.1), определяемой полярными координатами R и β, находится величина нормального напряжения σR, действующего по направлению радиуса R, а затем по формулам перехода – и все составляющие напряжения для площадки, проведенной через точку М, параллельно ограничивающей плоскости.
Для упрощения вывода (окончательный результат которого полностью совпадает с решением Буссинеска) принимается как постулат, что напряжение σR пропорционально cos β и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R2.
Тогда
|
(3.3) |
где А – некоторый коэффициент, определяемый из условия равновесия.

Рис. 3.1. Схема действия сосредоточенной силы.
Для составления уравнения равновесия проводится полушаровое сечение с центром в точку приложения сосредоточенной силы (рис. 3.2). Величина напряжений, нормальных к полушаровой поверхности, определяется выражением (3.3) и будет изменяться от нуля у ограничивающей плоскости до максимума по оси Z, но для выделенного элементарного шарового пояса с центральным углом dβ может приниматься постоянной.
Условием равновесия является сумма проекций всех сил на вертикальную ось, равная нулю:
|
(3.4) |
где dF - поверхность элементарного шарового пояса, равная:
Подстановкой выражения для dF и σR в уравнение (3.4), находится:
После интегрирования и подстановки пределов, имеем:
откуда находится неизвестный коэффициент пропорциональности А:
Подстановкой формулы (3.7) в формулу (3.3) находится выражение для радиальных напряжений:
|
Рис. 3.2. Схема радиальных напряжений
при действии сосредоточенной силы.
Из
геометрических соотношений можно найти
величину радиальных напряжений
![]() ,
отнесенных к площадке, параллельной
ограничивающей плоскости и составляющей
с ней угол β:
,
отнесенных к площадке, параллельной
ограничивающей плоскости и составляющей
с ней угол β:
|
Принимая
во внимание, что
![]() =z/R
и подставляя
значение
=z/R
и подставляя
значение
![]() из выражения (3.8),
можно получить
из выражения (3.8),
можно получить
|
(3.9) |
Тогда
|
или, учитывая (2.9),
|
(3.10) |
Поскольку из геометрических соотношений
|
то
|
|
|
Таким образом,
для практических расчетов имеем выражение
для определения сжимающих напряжений
![]() для площадки, параллельной ограничиваюшей
плоскости:
для площадки, параллельной ограничиваюшей
плоскости:
где
|
(3.12) |
Для облегчения
расчетов служит таблица 7П значений
коэффициентов
![]() , применяемых в формуле для вертикальных
сжимающих напряжений в массиве грунта,
нормальных к площадкам, параллельным
ограничивающей полупространство
плоскости.
, применяемых в формуле для вертикальных
сжимающих напряжений в массиве грунта,
нормальных к площадкам, параллельным
ограничивающей полупространство
плоскости.
Нагрузки, передаваемые через гибкие фундаменты или насыпи. В этом случае нагрузки следуют деформациям поверхности массива и сжимающие напряжения на поверхности массива равны интенсивности нагрузки.
Как показано выше, в случае сосредоточенных сил, нормальных к поверхности полупространства, вертикальное сжимающие напряжение в точке М от одиночной силы Р (рис. 3.3) вычисляется по формуле Буссинеска (3.11).

Рис. 3.3. Напряжения на площадке, параллельной поверхности полупространства.
При нескольких сосредоточенных нагрузках, если Р1 ≠ Р2 ≠ Р3 ≠ … ≠ Рi ≠ … ≠ Рn, сжимающее напряжение в любой точке массива для аналогичных площадок может быть найдено простым суммированием:
|
(3.12 а) |
то же при условии Р1 = Р2 = Р3 = … = Рi = … = Рn,
|
(3.12 б) |
Линейная (погонная) равномерно распределенная нагрузка, нормальная к поверхности. Вертикальное сжимающее напряжение в точке М вычисляется по формуле:
|
(3.13) |
Обозначения указаны на рис. 3.4 значения коэффициента приведены в табл. 8П.

Рис. 3.4. Расчетная схема к формуле (3.13).
Нагрузка, равномерно распределенная по гибкой полосе. Вертикальное сжимающее напряжение в точке М вычисляется по формуле:
|
(3.14) |

Рис. 3.5. Расчетная схема к формуле (3.14).
Обозначения указаны на рис 3.5; значения коэффициента К3 приведены в табл. 9П. Значение угла β2 принимается со знаком плюс для всех точек М, лежащих вне пределов границ загруженной полосы, и со знаком минус для точек М, лежащих в этих границах.
Для точек, расположенных в осевой плоскости загруженной полосы, где β1 = β2 = β, формула (3.14) принимает вид:
|
(3.15) |
На рис. 3.6 показаны линии равных напряжений в линейно деформируемом массиве в случае плоской задачи.
Нагрузка, распределенная по гибкой полосе по закону треугольника. Вертикальное сжимающее напряжение в точке М вычисляется по формуле Цытовича:
|
(3.16) |

Рис. 3.6. Линии равных напряжений в линейно деформируемом массиве в случае плоской задачи: а – изобары σz; б - распоры σу; в – сдвиги τzx.
Обозначения указаны на рис. 3.7, значения коэффициента К4 приведены в табл. 10П.

Рис. 3.7. Расчетная схема к формуле (3.16).
Любая нагрузка по гибкой полосе, меняющаяся по закону прямой. При любых нагрузках, меняющихся по закону прямой – треугольной трапецеидальной, прерывистой прямоугольной и других, вертикальное сжимающее напряжение может вычисляться по формуле:
|
(3.17) |
где
![]() - функция относительных величин
- функция относительных величин
![]() ;
;
а – длина треугольной части эпюры нагрузки;
b – длина прямоугольной части эпюры нагрузки;
s – глубина рассматриваемой точки.
Величина J определяется по графику Остерберга (рис. 1П) как алгебраическая сумма коэффициентов, соответствующих нагрузке слева и справа от вертикали, проходящей через рассматриваемую точку.
Нагрузка, равномерно распределенная по прямоугольной площади. Сжимающее напряжение σz в любой точке, лежащей под центром тяжести загруженного прямоугольника, стороны которого равны, может быть вычислено по формуле Лява:
|
(3.18) |
где
![]() ,
остальные обозначения указаны на рис.
3.8.
,
остальные обозначения указаны на рис.
3.8.
Значения коэффициента
К5
(в СНИПе он обозначается как α)
берут из табл. 11П в зависимости от
значения отношений
![]() и
и
![]() .
.
Для вычисления напряжений в любой точке М, расположенной под нагруженным прямоугольником в его пределах или вне его контура, применяется метод угловых точек. Метод основан на том, что напряжение под углом загруженного прямоугольника на глубине z составляет 1/4 от величины напряжения под его центром на глубине z/2. Поэтому для вычисления угловых напряжений можно применить формулу:
|
(3.19) |
Значения коэффициента
К5
можно взять по табл. 11П, а величина m
принимается равной
![]() ,
но не
,
но не
![]() как в случае центрально напряжения.
как в случае центрально напряжения.
При использовании метода угловых точек любая точка М рассматривается как угловая для четырех сходящихся углами загруженных прямоугольников, а напряжение вычисляется как алгебраическая сумма напряжений от каждого их этих прямоугольников. При этом могут иметь место два принципиальных случая:
1.Точка расположена в контуре загруженного прямоугольника (рис. 3.9 а). В этом случае напряжение в точке М на глубине равно сумме напряжений в этой точке от нагрузки, переданной на отдельные прямоугольники:
σz=σ1І + σ2 І І + σ3 І І І + σ4 ІV. (3.20)
2.Точка расположена вне контура загруженного прямоугольника (рис. 3.9 б). В этом случае прямоугольник ABCD достраивают с таким расчетом, чтобы точка М* стала угловой (прямоугольник HBEM’). Вычисление сводятся к определению напряжения от прямоугольника НВЕМ’ за вычетом напряжений от «фиктивных» (достроенных) прямоугольников AHFM’ и СЕМ’G.
Для определения напряжений под загруженной площадью любой конфигурации может быть применен метод элементарного суммирования.


Рис. 3.8. Расчетная схема к формуле (3.18). |
Рис. 3.9. Расчетные схемы для определения напряжений: а – под центром загруженного прямоугольника; б – в точке, расположенной вне контура загруженного прямоугольника |
Для этого загруженную площадь делят на элементы, а распределенную нагрузку на каждый элемент заменяют сосредоточенным элементарными нагрузками, что позволяет использовать при расчете формулы для сосредоточенной нагрузки.
Сжимающее напряжение в точке М на глубине z можно определить согласно выражению:
|
|
где n – число элементов, на которые разделена загруженная площадь.
Влияние на
распределение напряжений анизотропии
полупространства.
Многие типы глинистых и песчаных грунтов
характеризуются анизотропией свойств.
Проявлением анизотропии является
неравенство модулей деформации,
вычисленных по вертикальному Еz
и горизонтальному Er
направлениям. В неясно слоистых грунтах
отношение
![]() обычно не превышает 1,2 – 1,5; в отчетливо
слоистых оно может достигать 2 – 2,5.
обычно не превышает 1,2 – 1,5; в отчетливо
слоистых оно может достигать 2 – 2,5.
Вертикально сжимающее напряжение в точке М от сосредоточенной силы Р с учетом анизотропии грунта можно вычислить по формуле:
|
(3.22) |
Значения коэффициента К6 приведены в табл. 12 П.
Сопоставление значений коэффициентов К в табл. 12П и табл. 7П показывает, что при < 1 наблюдается концентрация напряжений по сравнению с изотропным полупространством. При > 1 в зависимости от значения коэффициента бокового расширения может наблюдаться как концентрация, так и рассеивание напряжений. Концентрация напряжений возрастает с увеличением коэффициента бокового расширения.
При действии линейной нагрузки интенсивностью р в аналогичных условиях для вычисления вертикальных напряжений применяется формула:
|
(3.23) |
Значения коэффициента К7 приведены в табл. 13П.
Влияние на распределение напряжений неглубоко залегающего жесткого или слабого слоя. Наличие на небольшой глубине от поверхности нажимаемого жесткого слоя (скальных или полускальных грунтов) приводит к увеличению (концентрации) сжимающих напряжений по оси нагрузки. Для случая действия местной равномерно распределенной нагрузки (в условиях пространственной задачи) нормальные напряжения на контакте двух слоев могут быть вычислены по формуле:
|
(3.24)
|
Значения коэффициента К8 приведены в табл. 14П.
При наличии на некоторой глубине слабого слоя величину максимального сжимающего напряжения на контакте двух слоев при действии полосообразной равномерно распределенной нагрузки можно вычислить по формуле:
|
(3.25) |
Значения коэффициента К9 приведены в табл. 15П. Величина V в таблице представляется собой параметр, характеризующий соотношение свойств двух контактирующих слоев:
|
где Е1, Е2, μ1, μ2 – деформация показатели для отдельных слоев.
Распределение напряжений в массиве грунта изображается с помощью линий напряжений (изобар) или с помощью эпюр, как это показано на рис. 3.10.


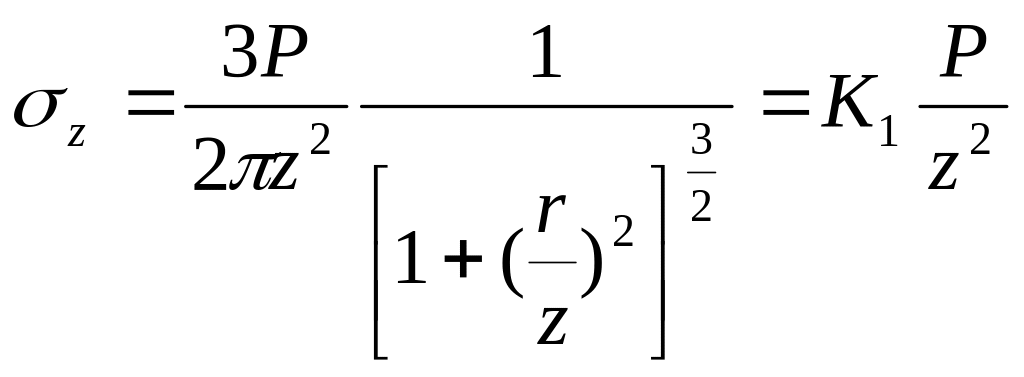 .
(3.11)
.
(3.11) .
.
 .
.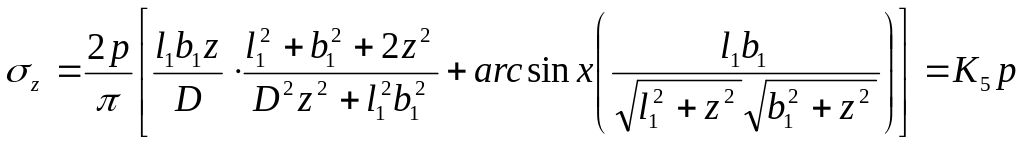 ,
,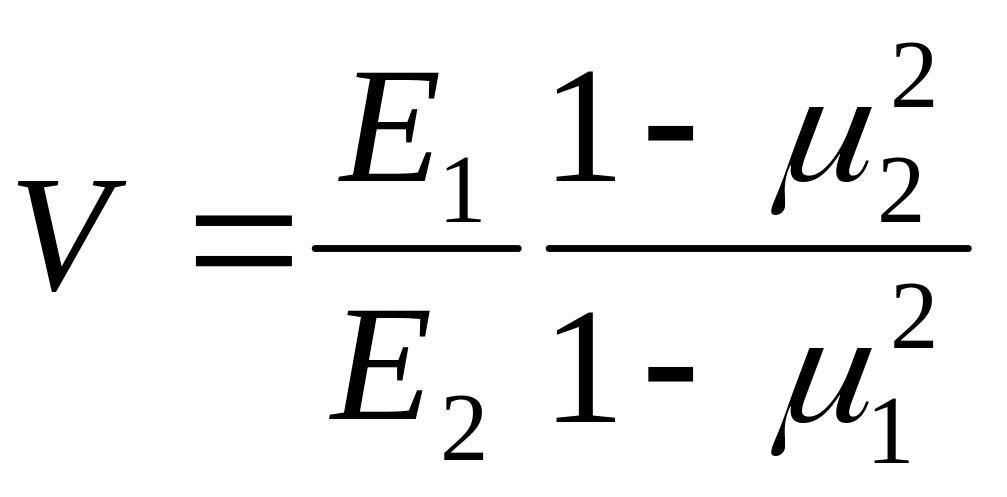 ,
(3.26)
,
(3.26)