
Унимодальная функция
.pdf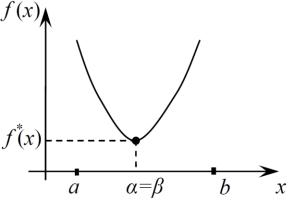
1.1. Унимодальность функции
Прежде чем приступить к оптимизации функции, необходимо определить, к какому классу она относится. Все исследуемые методы в
данной лабораторной работе применимы к унимодальным функциям.
Функция |
является унимодальной на отрезке |
, если она |
|||
непрерывна на интервале |
, и существуют числа |
, |
|||
такие что: |
|
|
|
|
|
1) |
строго монотонно убывает при |
(если |
); |
||
2) |
строго монотонно возрастает при |
(если |
); |
||
3) |
|
|
|
(inf – нижняя грань). |
|
Случаи, когда один или два из отрезков |
|
||
вырождаются в точку, здесь не исключаются. В частности, если |
, то |
||
функция |
строго унимодальная на |
(рис. 1). |
|
Рисунок 1 – Строго унимодальная функция на интервале |
|
||
Пусть |
унимодальная функция, |
заданная на интервале |
. При |
этом не требуется дифференцируемости |
и даже непрерывности |
функции |
|
. Введенное определение справедливо и для функции с разрывами и изломами. Из определения также следует, что унимодальная функция не
может содержать участков, где она постоянна. Примером унимодальной
функции может служить сильно выпуклая функция на интервале |
. |
Свойство унимодальности позволяет по результатам любой |
пары |
экспериментов указать интервал, в котором заключено значение , более узкий, чем начальный.
В зависимости от стратегии выбора двух точек и на интервале
имеются различные методы поиска минимум унимодальной функции,
отличающиеся скоростью стягивания интервала неопределённости, который содержит , к точке .
При решении практических задач в большинстве случаев функции не унимодальны. В этом случае рекомендуется следующий подход. Пусть
задана функция |
одной |
переменной |
, для которой допускается |
|
существование |
минимумов на интервале |
. |
||
Определим функцию: |
|
|
||
|
̅ |
∑ |
̅ |
|
|
|
|
{ |
|
|
|
|
|
|
По своему построению |
функция |
̅ унимодальна. Для получения |
||
решения в этом случае предлагается следующая организация вычислений:
1) |
Задание начальных значений поиска |
|
; |
|
||
2) |
Минимизация функции |
̅по |
|
, причем |
изменяется в |
|
|
своем интервале; |
|
|
|
|
|
3) |
Анализ |
результатов |
минимизации, |
при |
необходимости |
|
|
корректировка начальных значений |
|
и возврат к п. 2. |
|||
Полноту решения описанной процедуры обеспечивают стратегии: |
||||||
1. |
Случайное заданное |
точек на интервале поиска, где – |
||||
ожидаемое число |
минимумов |
функции |
. |
Минимизация при этом |
||
осуществляется итеративно на основе ряда последовательных реализаций случайного распределения точек с последующим объединением результатов итерации.
2. |
Равномерное назначение точек с последующей минимизацией |
и дальнейшим разбиением подинтервалов поиска по мере локализации
минимумов.
