в любом поисковом сервере картинку по ключевым словам «ХПИ логотип», наведите курсор мыши на найденный логотип, вызовите правой кнопкой контекстное меню, скопируйте картинку в буфер обмена, переключитесь на SMath Studio и вставьте картинку в документ.

Изображение можно перемещать и изменять его параметры. Сохраните документ как «SM16 рисунок.smz».

12.2.8. Решение технических задач

Решение обратной задачи с использованием функции solve()

В новом документе введите функцию, возвращающую объём шара

идентификатора Vшара используйте точку), необходимо определить, какой

диаметр имеет шар ёмкостью один литр. Введите «V:=10–3» (в системе СИ в м3), «d:=solve(Vшара(d) – V; d; 0; 1)», «d=» (м), «Vшара(d)=» (м3).

Первым аргументом функции solve( ) введено выражение, где разница между функцией Vшара(d) и заданным значением V приравнивается к нулю. В конце вычисления производится проверка. Сохраните документ как «SM17 обратная задача.smz».

Аппроксимация Аппроксимация, или приближение – научный метод, состоящий в

замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны).

Регрессия (лат. regressio – обратное движение, отход), в теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Функция, описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии.

В технике постоянно приходится проводить расчёты, в которых используются точные величины физических параметров. Соответствия

331

этих параметров (например, значения плотности жидкости при разной температуре) находят экспериментально и размещают в таблицах, т.е. значения являются дискретными. В вычислениях же необходимо использовать как можно более точные данные, обычно расположенные между точками значений таблиц. Кроме того, в вычислениях удобно использовать функции, возвращающие значения в зависимости от значения аргумента. Возникает задача получить из набора данных некую функцию, как можно точнее описывающую зависимость. В качестве такой функции часто используется полином (описывался в предыдущей работе). В некоторых случаях в качестве функции используются степенная и логарифмическая функции. Полином первой степени представляет собой прямую, что удобно использовать для описания линейных зависимостей без изменения алгоритма.

Задача сводится к поиску коэффициентов полинома. Чем больше значение коэффициента, тем больший вес в уравнении имеет соответствующий член полиномиальной зависимости. Не рекомендуется использовать степень аппроксимирующего полинома выше 4—6, т.к. сильно возрастают погрешности.

Полиномиальная регрессия – приближение данных полиномом, т.е. нахождение промежуточных значений с помощью полинома. Для построения регрессии полиномом k-ой степени необходимо наличие, по крайней мере, (k+1) точек данных.

Интерполяция, интерполирование – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Дискретный набор данных имеет граничные значения (минимум и максимум аргумента), интерполяция позволяет находить промежуточные значения внутри описанного дискретным набором данных диапазона.

Экстраполяция, экстраполирование (от экстра... – вне, снаружи, кроме и лат. polio — приглаживаю, выправляю, изменяю) – особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями. Т.е. экстраполяция использует полученную функцию для нахождения значений, когда аргумент находится за пределами исследованной области. При описании свойств веществ экстраполяцией можно пользоваться, если вы знаете, что

332

полученный результат с максимальной вероятностью достоверен. Например, построена таблица, описывающая зависимость динамической вязкости воды от температуры в интервале +20—+80°C при нормальном давлении. Экстраполяция по уравнению регрессии для указанного интервала, используемая для температуры ниже 0°C и выше +100°C заведомо не достоверна, так как изменяется агрегатное состояние воды. Также необходимо учитывать, что вещества могут разлагаться, а растворы кристаллизоваться. Если вы уменьшите масштаб графика приведённого ниже примера, то увидите, что за пределами исследованного диапазона функция может вести себя совсем не так, как вы ожидали.

В примере ниже задаются вектора исходных данных X и Y (транспонированы для уменьшения занимаемого места), степень полинома k. Далее определена функция пользователя pregress(X; Y; k) (полиномиальная регрессия), которая сначала проверяет соответствие размеров X и Y, затем строит матрицу F, содержащую степени X от 0 до k. Затем произведение матриц дает вектор коэффициентов полинома.

Вектор коэффициентов полинома вычисляется и присваивается в B, по нему строится полином P( ). Функцией matrix( ) создаётся пустая матрица Source из пяти столбцов, которая дополняется снизу функцией stack( ) строками, описывающими исходные точки данных на графике. Функция полинома и матрица исходных данных объединяются в систему diagram, по которой строится график. Ниже вычисляется дисперсия D (среднее значение квадрата отклонения случайной величины от своего среднего, характеризует степень разброса значений случайной величины вокруг её математического ожидания) и среднеквадратическое отклонение σ (численная оценка, вычисляемая по выборке – чем меньше, тем лучше в данном случае). Исходные данные можно загружать из файла функцией importData( ).

333

334

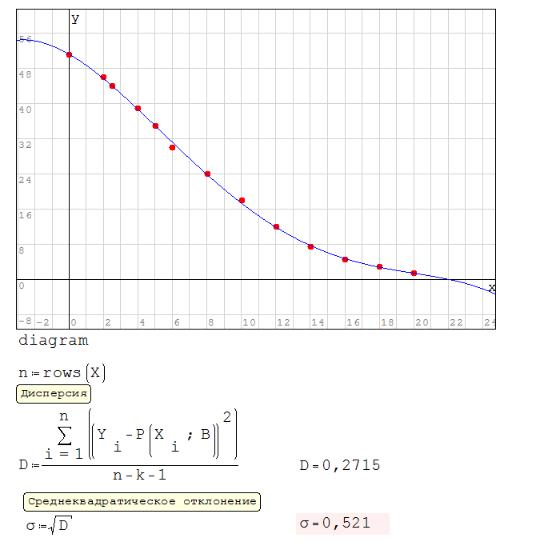
Исследуйте влияние степени полинома k в интервале 1..6 на вид графика и величины качественных показателей уравнения регрессии (среднеквадратического отклонения), при каждой итерации выводите заново значение σ и отключайте вычисления для этого блока. Запишите в лабораторный журнал коэффициенты полинома и σ для всех шести случаев в виде таблицы. Сохраните документ как «SM18 регрессия.smz».

Вопросы к подготовке:

1.Как найти корни функции?

2.Как найти решение системы уравнений?

3.Что такое символьные вычисления?

4.Как написать программу? Опишите структурные операторы.

5.Для чего используется аппроксимация?

335