Сохраните документ как «SM13 программы.smz».

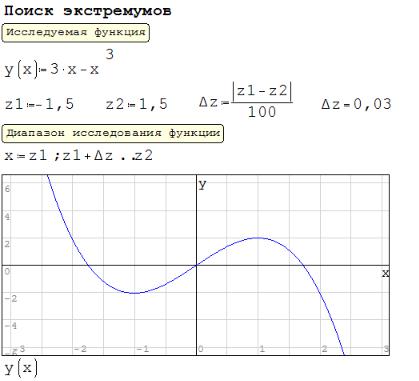
12.2.6. Поиск экстремума

Необходимо найти экстремум (минимум или максимум) функции y(x). Если известно, что функция монотонна и у функции один экстремум в рассматриваемой области, то можно воспользоваться простым алгоритмом перебора значений для векторов решений, выполненных с малым шагом. Для исследования примем достаточным разбиение исследуемого интервала на сто отрезков. Исследуемую функцию назовите y(x), соответственно изменяемый параметр x, начало, конец и шаг параметра: z1, z2 и z. На масштабированном графике можно визуально определить количество экстремумов в исследуемом диапазоне. Обратите внимание, что границы диапазона исследования в примере заданы так, чтобы абсолютное значение функции в них было меньше абсолютного значения экстремумов. Метод перебора находит максимальное и минимальное значение в последовательности, и сам не может найти точки перегиба функции. Точки перегиба можно найти, добавив в алгоритм проверку, что обе соседние точки одновременно меньше или больше текущей. В новом документе повторите пример:

327

Впримере создана функция Maximize(y(a);x), которая последовательно перебирает с заданным шагом значения исследуемой переменной, подставляя в исследуемую функцию, чьё значение сравнивается с ранее сохранённым максимумом. Если текущее значение больше сохранённого, то оно и его позиция сохраняются в переменные. Функция в качестве результата возвращает вектор координат максимума «x; y». Точность поиска равна шагу z. Если на исследуемом диапазоне присутствуют несколько одинаковых максимумов, то функция возвращает первый найденный. Функция помещена в область, чтобы её можно было свернуть. Заметьте, что функция y(a), а точнее ссылка на функцию, использует в качестве формальной переменной а, так как нельзя использовать переменную x создаваемой функции Maximize в качестве параметра функции-аргумента.

Создайте ниже копию последних двух блоков и области, замените в них название функции Maximize на Minimize, имя локальной переменной Max (отличается от имени функции max( )) на Min, и оператор сравнения

строго больше «>» в операторе if на оператор строго меньше «<».

Сохраните документ как «SM14 экстремумы.smz».

Вследующем примере рассмотрите поиск экстремума с помощью аналитического метода, принимая к сведению, что в точке экстремума

328

функции значение первой частной производной равно нулю (изменение знака производной в точке пересечения оси x с минуса на плюс указывает минимум функции, иначе – максимум).

Для решения используйте следующий алгоритм: задайте функцию, задайте производную от неё функцию, задайте границы интервала исследования, постройте графики функции и её производной (оставьте место для других выражений или по мере добавления выражений смещайте график ниже), корни производной функции дают X-координаты экстремумов, подстановка их в исходную функцию даёт Y-координаты.

Описания блоков при повторении примера можно не вводить.

329

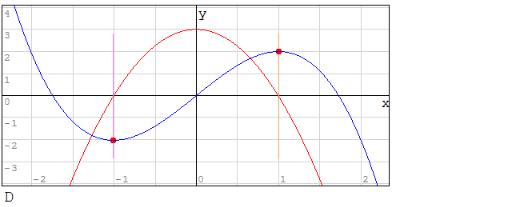
Отрезки, описываемые вложенными матрицами вектора r, служат для маркировки проекции экстремума на ось X в точку пересечения производной с осью (при количестве экстремумов, отличном от двух, соответственно нужно менять количество маркирующих отрезков в алгебраической системе), матрица ext используется для отображения точек экстремумов. Производная на графике представлена параболой. Функция solve( ) возвращает вектор корней (точек пересечения с осью X), присваиваемый в переменную x1. В первом цикле производится вычисление Y-координат экстремумов подстановкой найденных X-координат в исходную функцию. В этом же цикле заполняется массив ext, используемый для отображения (красных) точек на графике. Справа от первого цикла производится поиск максимального и минимального значения в списке экстремумов, находится расстояние между ними (Δy1), и для координат отрезков создаётся 20% (от y1) выступ по высоте.

Сохраните документ как «SM15 экстремумы.smz».

12.2.7. Вставка рисунка

В ряде случаев в документ необходимо вставить рисунок. Это можно осуществить командой меню Вставка/Рисунок/Из файла или с помощью буфера обмена. Также командой Вставка/Рисунок/Создать (Ctrl+T) можно вставить холст для рисования и надписей мышью. Вставьте шаблон рисунка, в нижнем левом углу блока введите в двойных кавычках путь "C:\WINDOWS\Web\exclam.gif" (в Windows 7 найдите и укажите путь к любому другому небольшому изображению в форматах PNG, BMP, GIF или JPG). На рисунке с помощью контекстной команды Правка можно рисовать мышью. Откройте программу обзора интернета, найдите

330