Исследуйте влияние степени полинома на вид графика и величины качественных показателей уравнения регрессии. Изменяйте степень полинома k в интервале 1..6.

12.2. SMATH STUDIO

12.2.1. Поиск корней

SMath Studio позволяет находить корни уравнения (нуля функции), т.е. точки, где значение функции равно нулю (графически пересекает ось X). Исследуйте выражение (набирать его так не нужно!) «x2+2x+1=0». Из этого выражения можно построить функцию «y(x):=x2+2x+1», введите её в новый документ. Постройте график этой функции. В правой части описания функции выделите переменную x, выполните команду Вычисление/Найти корни, найденные корни будут выведены ниже уравнения. Этот метод используется для оценки функции, но не сохраняет результат в переменную, для чего используется функция solve( ) (англ., решить). Более простой вариант функции solve( ) с двумя аргументами (первый задаёт функцию, а второй переменную, по которой ведётся поиск корней), как и команда Найти корни, ищет корни в заданном в настройках диапазоне (Сервис/Опции/Вычисление/Корни

313

(диапазон)), по умолчанию –20..20. Второй вариант функции solve( ) содержит четыре аргумента, где третий и четвёртый задают границы исследуемого диапазона. Для управляемого поиска предпочтительнее использовать вариант solve( ) с четырьмя аргументами. Введите «x1:=solve(y(x);x)», «x1=». В качестве первого аргумента функции solve( ) можно вписать непосредственно исходное выражение, и даже в виде равенства, но использовать вместо «равно» – оператора численного вывода, оператор сравнения «жирное равно» (Ctrl+=). В этом примере найден и выведен один корень в виде скаляра.

Необходимо найти решение уравнения ex=x3. Преобразованное выражение в функцию имеет вид «y(x):= ex–x3» (1). Введите функцию (1), ниже постройте её график (2), увеличьте размер полотна графика. Масштабируйте и перемещайте график до удобного просмотра области пересечения с осью X. Ниже графика вычислите и присвойте (3) переменной z корни выражения (1) для визуально определённого диапазона расположения корней 0..5. Выведите (4) значение z. В этом примере найдено два корня, которые отображаются в виде вектора. Вектор корней можно использовать в выражениях, в том числе циклических, опередив количество найденных корней как размер (количество элементов) вектора функцией length( ), введите «length(z)=»

(5). Рассмотрите дополнительную возможность комментировать вычисления – описания, выделите выражение (1), в контекстном меню выполните команду Отображать описание, над выражением появится выделенный цветом блок, впишите в него текст «Исследуемая функция». Для графика (2) задайте описание «График функции y(x)». Выражению

(3) введите описание «Поиск корней», выражению (4): «Корни функции y(x)», выражению (5): «Количество корней». Описание отличается от текстовых блоков тем, что перемещается вместе с выражением, формат описания нельзя изменить, описание можно скрыть без потери содержимого и показать, что удобно для создания учебных документов или документов для новичков. Выделите блоки с описаниями, в контекстном меню отключите Отображать описание. Сохраните документ как «SM08 корни.smz».

314

В новом документе аналогично предыдущему примеру, с построением графика и использованием функции solve( ) с четырьмя аргументами самостоятельно найдите корни выражения x3=10x–2.

Преобразование выражения предыдущего абзаца даёт функцию y(x):=x3–10x+2, которая является полиномом108, у которого значение коэффициента C2 у x2 равно нулю (y(x)=x3+0∙x2–10x+2). Существует функция polyroots( ), которая возвращает вектор всех нулей полинома (как действительных, так и комплексных). Аргументом функции polyroots( ) является вектор коэффициентов, заданный без пропусков (нулевые коэффициенты задаются явно) в порядке возрастания номера (степени переменной, при которой находится коэффициент).

(многочлен) – функция одной переменной вида f(x)=C0+C1x+…+Cnxn, где ci фиксированные коэффициенты, а x – переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе. Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства, способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе. Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов. При употреблении полинома принято указывать его степень, равную максимальной степени переменной в выражении, в рассматриваемом примере используется полином третьей степени. Полиномы степеней 3–6 популярны в программах технологических расчётов из-за простоты использования и точности описания свойств веществ, где коэффициенты полиномов описания свойств заданы массивами констант.

315

Переменной С присвойте вектор (столбец), содержащий перечень коэффициентов полинома 2; –10; 0; 1. В этом примере, как указывалось ранее, коэффициент C2 равен нулю (расположен в третьей строке, так как нумерация коэффициентов начинается с нуля), что отражено в векторе коэффициентов и C2x2 отсутствует в уравнении. Ниже введите «polyroots(C)=», будет выведен вектор, содержащий корни полинома. Сравните со значениями, полученными с помощью функции solve. Использование функции polyroots( ) предпочтительнее solve( ), т.к. не требуется задавать границы поиска, для полинома любой степени можно написать универсальную формулу, что будет рассмотрено далее. Функция solve( ) возвращает только вещественные корни, функция polyroots( ) также может возвращать комплексные корни. Сохраните документ как «SM09 полином.smz».

12.2.2. Решение систем уравнений, функция roots( )

Напоминание: имена массивов принято задавать с заглавной буквы, что упрощает распознавание выражений, а переменных со строчной.

a 2b 3c 1

Система алгебраических линейных уравнений вида 4a 5b 6c 27a 8b 9c 3

может быть записана в матричной форме: A ∙ X = B, где A – квадратная матрица коэффициентов при неизвестных, X – вектор неизвестных, B – вектор свободных членов. Решить такую систему линейных уравнений можно операцией A–1∙B – произведение обратной (инвертированной) матрицы на вектор свободных членов B. В этом примере используется «телефонная матрица», повторяющая раскладку кнопочного телефона, довольно часто используемая для примеров.

В случае если матрица вырождена (сингулярна), т.е. её определитель равен нулю, вычисление прервётся ошибкой.

3a 2b 1c 4

8a 5b 9c 6

Необходимо найти решение системы уравнений .7a 4b 6c 9

В новом документе создайте матрицу A 3 3 (заполните значениями: 3; 2; 1; 8; 5; 9; 7; 4; 6), создайте вектор B из трёх элементов (4; 6; 9).

316

введите выражения «X := A–1 ∙ B», «X =», выполните проверку: «A ∙ X =», результат должен совпасть со значениями свободных членов (вектор B).

Для решения систем уравнений, в том числе нелинейных, используется функция roots( ), которая использует две формы – с двумя и тремя аргументами. Аргументами являются вектора одинакового размера, первый вектор содержит уравнения, второй – список переменных, для которых производится поиск значений, при которых функции первого аргумента равны нулю. Третий аргумент может содержать значения начальных приближений. Задание начальных приближений во многих случаях необходимо, если система имеет несколько решений. Уравнения можно перечислять непосредственно в аргументах-векторах функции, а можно задать в качестве отдельных функций. Вектора списка переменных и начальных приближений также можно передавать с помощью переменных.

Для получения уравнений системы необходимо правую часть равенства перенести в левую часть. Создайте список переменных, введите v, присвойте вектор из трёх строк, в который введите a; b; c. Создайте функцию «F(a; b; c) := A ∙ v – B», выведите её значение символьно (Ctrl+точка), отключите оптимизацию для блока вывода, сравните полученную систему с исходной. Найдите решение системы, введите «X1 := roots(F(a; b; c); v)», «X1 =». Сравните полученные разными методами вектора решений X и X1.

Решите задачу: при каких значениях x выражения x2+10 и ex приобретают одинаковые значения (т.е. когда x2 + 10 = ex)? Введите функцию «roots(x2 + 10 = ex; x; 1) =», где используется «жирное равно» (Ctrl+=) – оператор эквивалентности, его также можно ввести из группы Булева боковой панели.

Сохраните документ как «SM10 системы уравнений.smz». Рассмотрите пересечение окружности с прямой. В новом документе

задайте радиус r, равный четырём, добавьте блоку описание «Радиус окружности». Переменной a присвойте значение 1,5, добавьте описание «Наклон прямой». Переменной h присвойте 2 и описание «Сдвиг прямой». Выделите блоки (при нажатой левой кнопке мыши передвигайте курсор, чтобы выделяемые блоки попали в выделяющую область), вызовите команду Цвет фона панели инструментов, выберите

317

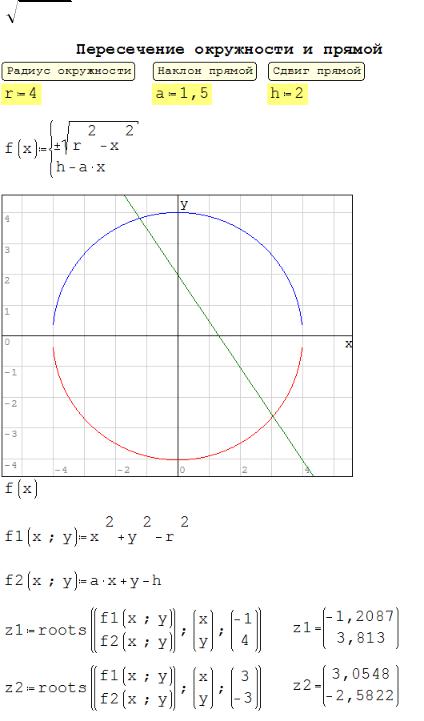
светло-жёлтый цвет. Выделение цветом обычно используется для пометки полей ввода исходных данных. Постройте график, как показано ниже, для создания окружности (x2 + y2 = R2) используются два графика для верхней и нижней половины с использованием оператора «±»: «

y 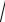r2 x2 ». Прямая задана уравнением «y = h – a ∙ x».

318