курсор в позицию перед оператором Find (оператор подчёркнут и курсор перед словом, переключать положение за- и передсловом можно клавишей Insert), нажмите «:» (вставится :=), введите в маркер ввода f(R). Ниже вызовите новую функцию с разными аргументами и выведите значения: «f(R) =», «r := 2.5, 2.6 .. 3», ниже «r = f(r)0 = f(r)1 =» (у функции указывается индекс для вывода отдельно вектора x и y). Сохраните документ как MC14.xmcdz.

Mathcad содержит функцию MinErr(), очень похожую на функцию Find(). Функция Minerr() использует тот же самый алгоритм, что и функция Find(). Различие состоит в том, что если в результате поиска решения не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr() возвращает это приближение, а функция Find помечается сообщением об ошибке «решение не найдено».

12.1.3. Символьные вычисления

Оптимизация вычислений

Некоторые численные операции в Mathcad довольно длительны (например, вычисление двойного или тройного интеграла). Для ускорения вычислений в пакет встроена оптимизация вычислений, которая предполагает попытку символьного упрощения выражения перед численным вычислением. В результате символьного преобразования может получиться выражение, требующее значительно меньших затрат ресурсов и времени. Оптимизация допускается для выражений, использующих оператор присваивания «:=». Оптимизировать выражение с оператором присваивания можно командой меню Сервис/ Оптимизировать/ Уравнение или командой контекстного меню Оптимизировать. При включённом режиме у выражения справа появляется звёздочка – синяя, если оптимизация не нужна и красная при использовании оптимизации.

Аналитические преобразования

Ранее в результатах расчёта вы получали отдельные числа или наборы чисел. Mathcad обладает возможностью производить также символьные вычисления, т.е. вычисления, в результате которых получается формула (функция).

297

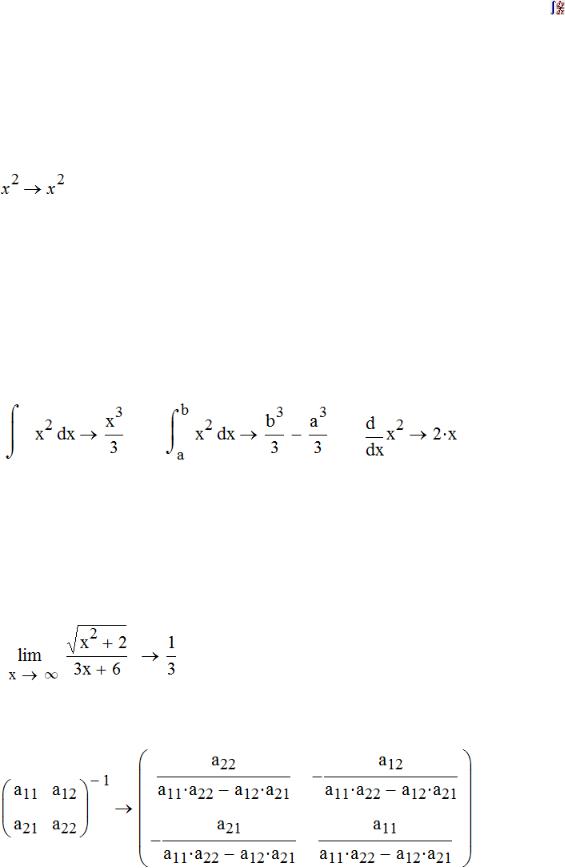
Откройте панель Символьные преобразования и панель

Математический анализ. Для символьного преобразования (символьного вывода результата) необходимо ввести исходное выражение, затем нажать кнопку Аналитические преобразования на панели с изображением «стрелка вправо» или сочетание клавиш Ctrl+точка. Если введённое выражение не удаётся преобразовать (упростить), оно остаётся неизменным. В новом документе введите «x2», вызовите оператор

Аналитические преобразования (Ctrl+.), нажмите Enter:

На панели 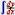Математический анализ нажмите кнопку неопреде-

лённого интеграла (Ctrl+I), в маркеры ввода шаблона интеграла впишите функцию «x2» и переменную интегрирования «x», затем выполните символьный вывод. Правее вставьте шаблон определённого интеграла (&), в шаблон впишите значения нижнего и верхнего пределов – a и b, в качестве функции также укажите «x2» и переменную интегрирования «x», затем выполните символьный вывод. Аналогично правее символьно выведите производную функции «x2» по переменной дифференцирования «x»:

Самостоятельно, используя команды панелей Математический анализ и Символьные преобразования, найдите для этой же функции символьное решение производной второй степени и двойного интеграла.

Найдите предельное значение функции. Нажмите кнопку

Двусторонний предел (Ctrl+L) панели Математический анализ. В маркер ввода слева внизу оператора lim впишите «x», правее стрелки – «∞», в маркер ввода введите выражение и нажмите Ctrl+.

Ниже вставьте матрицу 2×2, заполните именами ячеек a11, a12, a21, a22, выполните команду Обращение панели Матрица, выведите результат в символьном виде:

298

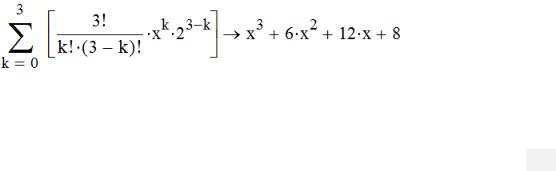
Символьные преобразования с ключевым словом

Символьные преобразования позволяют упростить выражения, введите (при вводе следите, чтобы набор осуществлялся в блоке внутри суммы, скобки вставляются автоматически):

При задании функции, Mathcad хранит её «как есть», не проводя преобразований. С помощью ключевых слов оператора символьного преобразования можно достичь разных результатов. Для преобразования вводится выражение, затем, не покидая блока, нажимается кнопка ▪ →

Символьный расчёт с ключевым словом (в подсказке к команде указано

Ctrl+>, т.к. символ «→» вызывается Shift+., необходимо нажать Ctrl+Shift+.) и в маркер ввода вписывается ключевое слово и другие параметры. На панели Символьные преобразования есть кнопки с ключевыми словами, которые одновременно также отображают оператор символьного вывода (→).

Задайте функцию «y(x):=(x4 – 16)/(x2 + 4)», ниже введите «y(x)», нажмите кнопку simplify (Упростить выражение), нажмите Enter. Ниже повторите символьные преобразования функции y(x) с ключевыми словами factor (Разложить выражения на множители), expand (Развернуть выражения).

Самостоятельно для выражения «(x + 3) ∙ (2x + 4)» проведите операции Упростить, Развернуть, Разложить на множители и получить Полиномиальные коэффициенты.

Тандемы операторов

Для одновременных операций вычислений, преобразований и присваивания в Mathcad имеется возможность тандема операторов. Удобно использовать тандемы операторов символьных преобразований и численного вывода, присвоения и символьного преобразования, присвоения и численного вывода.

Найдите корни уравнения с использованием символьного решения и тандема с численным выводом (см. пример ниже). Задайте функцию полинома, ниже приравняйте (Ctrl+=) функцию нулю, и выставьте оператор символьного решения solve, после него выставьте запятую и

299

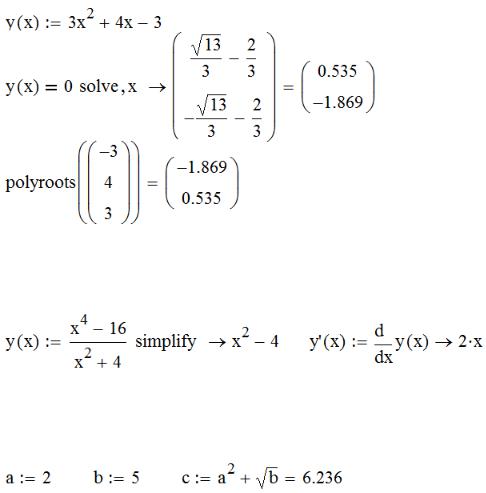
переменную «x», нажмите Enter, выделите выражение повторно и нажмите =. Проверьте решение с помощью функции polyroots().

Использование операторов символьных преобразований совместно с присвоением позволяет присваивать уже преобразованное выражение. Выполните примеры:

И достаточно удобно использовать оператор присвоения (для дальнейшего использования результата) и численного вывода (для контроля выполнения).

Поиск экстремума

Необходимо найти экстремум (минимум или максимум) функции y(x). Если известно, что у функции один экстремум в рассматриваемой области, то можно воспользоваться функциями Maximize() и Minimize(), в новом документе повторите пример:

300

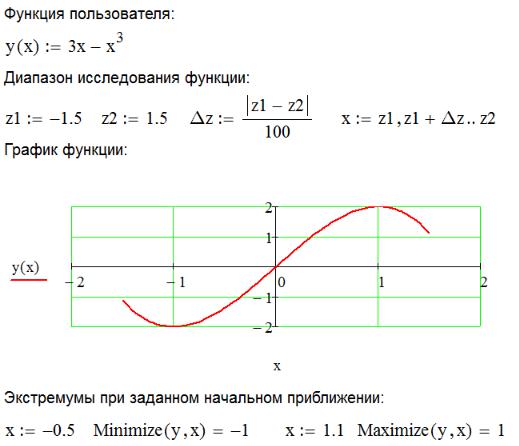
Для нахождения экстремумов также можно использовать графический метод (нажмите кнопку панели График – Трассировка, поместите курсор на график, нажмите и удерживайте левую кнопку мыши, перемещайте курсор вдоль линии графика).

И третий, аналитический метод с использованием символьных вычислений с поиском корней производной функции (в точке экстремума функции значение первой частной производной равно нулю).

Для решения используйте следующий алгоритм: задайте функцию, определите её производную (для ввода штриха в имени функции y' используйте символ «`», клавиша которого расположена в верхнем левом углу клавиатуры), задайте интервал исследования, постройте графики функции и её производной (оставьте место для других выражений или по мере добавления смещайте график ниже), в точках пересечения производной оси X найдите корни (координаты X экстремума), подстановкой их в исходную функцию получите Y-координаты экстремумов, введите вспомогательные отрезки для обозначения точек экстремума. Отрезки x1extr/yextr и x2extr/yextr служат для маркировки

301

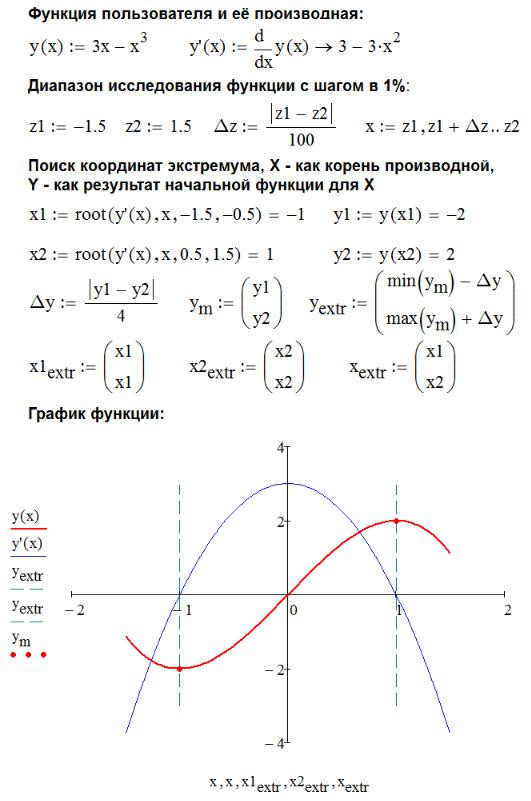
проекции экстремума на ось X в точку пересечения производной с осью, отрезок xm/ym не воспроизводит линии, а выводит символ узла, и показывает точки экстремумов.

302