11.2.7. Дискретные переменные, массивы

Одиночное число называется скаляром98. Столбец чисел называется вектором, а прямоугольная таблица чисел – матрицей. Общий термин для вектора или матрицы – массив.

SMath Studio позволяет задавать переменные с пределами изменения. Фактически дискретная переменная (в некоторых источниках её также называют ранжированной) является набором чисел в заданном интервале с постоянным шагом приращения значения. Для создания дискретной переменной, ей присваивают диапазон значений, состоящий минимум из значения Начало_диапазона, оператора диапазона – двойной точки, горизонтального двоеточия (..) и значения Конец_диапазона. В этом случае шаг приращения по умолчанию равен единице. Диапазон задаётся функцией range( ), которая автоматически переводится в вид «n1..n2» или «n1;n3..n2» в зависимости от количества параметров функции – два или три. Третьим параметром может быть задан шаг изменения, который по умолчанию, если не задан, принимается равным единице.

Создайте новый документ командой Файл/Создать лист (Ctrl+N) или первой кнопкой панели инструментов, для получения выражения присвоения дискретной переменной «m := 0 .. 9» посимвольно введите «m:range(0;9», численно выведите значение m, должен быть выведен вектор значений от 0 до 9 с шагом 1. Для указания шага, отличного от единицы, используют схему диапазона элементов «Первый, второй .. последний», шаг вычисляется как разницу между вторым и первым элементами последовательности. Установите красный маркер правее присваивания переменной m, заданной ранее. Введите выражение «x := – 1; –0,8 .. 1» (посимвольно: «x:range(-1;1;-0,8», третий аргумент будет вставлен через точку с запятой после первого), ниже выведите значение

98 Скаляр (от лат. scalaris – ступенчатый) – величина (возможно переменная, то есть функция), каждое значение которой может быть выражено одним числом (чаще всего подразумевается действительное число). При смене системы координат скаляр остаётся неизменным (инвариантным), в отличие, например, от компонент вектора, которые могут быть разными у одного и того же вектора в разных системах координат.

278

x. Из-за специфики хранения вещественных чисел, дробный ноль может отображаться очень малым числом. У дискретной переменной x шаг значений задан разностью –0,8 и –1, и составляет 0,2. Проведите ещё один эксперимент с дискретными переменными. Справа от присвоения x введите выражение с помощью функции range( ) «y := 0; 0,3 .. 2», ниже выведите значение y. Как видно, шаг не кратен диапазону, поэтому значение верхней границы выпадает из списка и последнее значение равно 1,8.

Если аргументом функции является дискретная переменная, результатом будет вектор. Задайте дискретную переменную z в диапазоне – 0,5π по 0,5π с шагом 0,3: «z := –0,5π; –0,5π + 0,3 .. 0,5π». Так как функция в SMath Studio обрабатывает скаляр, для обработки вектора необходимо вызвать функцию для каждого элемента, это позволяет реализовать структура цикла. Наберите на клавиатуре оператор цикла for, в списке динамической помощи ввода выберите вариант for(3), в котором присутствуют три маркера ввода: первый определяет переменную – счётчик цикла, второй границы цикла с помощью дискретного диапазона и третий – выражение, выполняемое внутри цикла заданное количество раз. В первый маркер введите «i», во второй маркер введите диапазон с использованием функции range( ) «1 .. rows(z)», где функция rows( ) возвращает размер вектора z (количество строк). В третий (нижний) маркер введите «Si:=sin(zi)», для задания индекса S и z используйте кнопку el (element) группы Функции боковой панели или, что проще,

открывающую квадратную скобку, после ввода индекса необходимо

вернуться на основной уровень формулы клавишами пробел или вправо:

z:=-0,5∙π;-0,5∙π+0,3..0,5∙π for i 1..rows(z)

Si:=sin(zi)

Выйдите из блока клавишей Enter и выведите вектор значений «S=». Самостоятельно задайте и выведите значения дискретной переменной w в диапазоне от –5 до 5 с шагом 0,25.

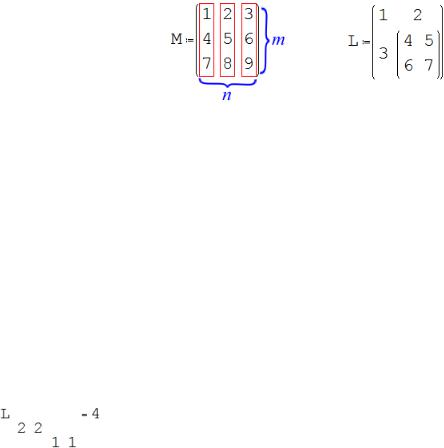
Матрицы можно рассматривать как n одномерных массивов, каждый из которых имеет m элементов (Рис. 11.1а). Массивы, элементы которых являются массивами называются составными (Рис 11.1б).

279

Векторы и матрицы имеют имена и характеризуют совокупность значений ряда их элементов. Элементы векторов характеризуются порядковым номером или индексом. Например, если задан вектор V, то его элементами будут V1, V2 и т.д., в общем виде Vi, где i – индекс. Нумерация идет с единицы. Матрицы имеют элементы с двумя индексами, первый из которых указывает на номер строки, а второй – на номер столбца. Например, если задана матрица М, то её элементами будут М1,1, M1,2, М2,3 и т.д., в общем виде Мi,j.

Для обращения к элементу вложенной матрицы составного массива сначала указывают адрес во внешней матрице, а затем во внутренней:

Для задания матрицы установите курсор на место ввода, введите «M :=», вызовите команду Вставка/Матрица (Ctrl+М) или кнопкой Матрица 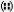группы Матрицы боковой панели. Укажите число строк 3 и число столбцов 3. Заполните матрицу числами (1, 3, 6, 4, 7, 5, 2, 9, 8), перемещаясь по маркерам ввода элементов матрицы с помощью клавиш влево/вправо. Для изменения размера матрицы (удаления/добавления строк/столбцов) необходимо выделить всю матрицу, в правом нижнем углу рамки матрицы появится маркер масштабирования, за который можно курсовом мыши менять размер матрицы. При уменьшении размера содержимое ячеек теряется.

Для получения значения отдельного элемента, обратитесь к нему по индексу. Введите «M [ 1; 3 =», появится M1 3 = 6 (ниже в работе для указания индекса массива используйте открывающую квадратную скобку, точка используется для записи части имени в подстрочном положении и к индексам отношения не имеет). Отсюда следует, что

280

первый индекс указывает строку 1, а второй – столбец 3. Введите M, нажмите кнопку Транспонирование99 ■T (Ctrl+1) и затем равно.

Для вычисления определителя100 матрицы введите имя функции

«det(» или нажмите кнопку Определитель матрицы группы Матрицы

боковой панели, появится пара вертикальных линий, в маркер ввода между которыми впишите имя матрицы M и нажмите равно.

Вычислите сумму всех элементов матрицы M – введите sum, в списке динамического ввода выберите функцию вычисления суммы всех элементов массива sum(1), нажмите Tab для вставки, в маркер ввода введите M, нажмите равно. Сумму можно вычислить по строкам и по столбцам: введите sum, в списке динамической помощи выберите sum(4), повторите операцию для вставки вложенной суммы (можно использовать кнопку Функция итерационной суммы группы Функции боковой панели).

Под первым знаком суммы введите i = 1, под вторым j = 1, над каждым из них тройку, в маркер ввода справа знаков сумм введите Mi j и нажмите =.

столбцов в строке, считает сумму строки, а первая, внешняя сумма, суммирует полученные суммы строк. Используя единственную функцию итеративной суммы, самостоятельно вычислите сумму элементов главной диагонали матрицы M.

Извлеките последний столбец матрицы: введите «col(M;cols(M))=» (функция cols( ) возвращает количество столбцов матрицы). Извлеките первую строку: введите «row(M;1)=».

99 Транспонированная матрица – матрица AT, полученная из исходной матрицы A заменой строк на столбцы.

100 Определитель (или детерминант) – многочлен от элементов квадратной матрицы. Определитель матрицы А обозначается как: det(A), |А| или Δ(A). Для матрицы n×n определитель задаётся рекурсивно:

n

( 1)1 j a1 j M 1j , где M 1j – дополнительный минор к элементу a1j. При

j 1

транспонировании определитель матрицы не изменяется. 281

Спомощью обычной операции умножения вычислите скалярное101

произведение и с помощью команды Оператор векторного умножения 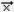(Ctrl+8) группы Матрицы боковой панели вычислите векторное102 произведение первого и второго столбца матрицы M.

Спомощью функций min( ) и max( ) найдите значения минимального

имаксимального элементов матрицы M.

Сохраните документ под именем «SM02 матрицы.smz». Дополнительные функции для работы с матрицами и векторами

можно найти в окне Функции, категория Матрицы и векторы, а также обсуждение использования изучить на форуме программы.

Ниже приведён пример использования векторов для рекурсивных расчётов. Введите пример в новый документ, сохраните его именем «SM03 итерации.smz». Для вычисления в цикле нескольких выражений используйте оператор Добавить строку (line) группы Программирование

боковой панели (также можно ввести «line(» или нажать «]»). Если выделить пробелом или стрелкой вправо всю линию программирования, то за появившийся в правом нижнем углу маркер масштабирования можно менять количество полей ввода линии, добавить один маркер в линию программирования можно точкой с запятой.

101Скалярное произведение – операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы

координат и характеризующее длины векторов-сомножителей и угол между ними. a,b a b cos a,b

102Векторное произведение – это вектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции векторное умножение над векторами в трёхмерном Евклидовом пространстве. Векторное произведение полезно для «измерения» перпендикулярности векторов – длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны. Векторное произведение определено только в трёхмерном и семимерном пространстве. В отличие от скалярного произведения, векторное зависит от ориентации системы координат или, иначе, «хиральности».

282