2.2. Алгоритм вирішення з використанням методу дослідження функцій класичного аналізу

Площі поверхні теплообмінників можно знайти за допомогою рівняння теплопередачі:

• для теплообмінника-регенератора:

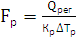
• для теплообмінника-підігрівача:

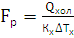
• для теплообмінника-холодильника:

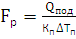
Q_рег, Q_хол, Q_под –теплові навантаженнятеплообмінників:

Q_под = G_xC_x(T_x^K – T_x^’)

Q_хол= G_гC_г(T_x^’ – T_x^К)

Q_рег= G_xC_x(T_x^’’ – T_x)

∆T_p, ∆T_П, ∆T_X, - розрахункові різниці температур :

∆T_X = 0,5(T_x^’ – T_x^К) – Т₀

∆T_П =T_гр 0,5(T_x^к – T_x^’)

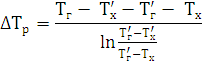
Для спрощення виразів введемо наступні значення:

T_Х^K-T_Х = δT_Х

T_Г-T_Г = δT_Г

0,5(T_Х-T_Х^K)= T_Х^СР

0,5(T_Г-T_Г^K )= T_Г^СР

Температури потоків на виході з теплообмінника-регенератора виразимо через відомі температури та ступень регенерації тепла:

К_р, К_П,К_Х – коефіцієнт теплопередачі відповідних теплообмінників.

Розрахунок коефіцієнтів теплопередачі можна провести таким чином:

• Розрахуємо площу перерізу трубного простору:

• Еквівалентний периметр тадіаметрміжтрубного простору:

П = π(D_K-nd_BH)

Необхідно відмітити, що в теплообміннику-підігрівачу сировина рухається по міжтрубному простору, а теплоносій що гріє – по трубному. В теплообміннику- холодильнику: дистилят – по трубам, вода – по між трубному простору. У теплообміннику-регенератору: сировина – по міжтрубному простору, а дистилят – по трубам.

• Знаходимо швидкості теплоносіїв:

Для визначення режиму руху теплоносія, визначимо критерії Рейнольдса:

По числу Re визначимо режим руху теплоносія та у відповідності з ним визначимо критерій Нусельта:

• Для турбулентного режиму:

• Для перехідного режиму:

Nu = 0.08∙ Re^0.9∙ Pr^0.43

• Критерій Прандля:

• Коефіцієнт тепловіддачі:

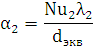
• Коефіцієнт теплопередачі:

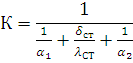
З урахуванням наведених раніше виразів та, маючи на увазі, що мінімуму змінної частини річних (приведених) зведених витрат відповідає рівняння нулю першої похідної та достатнього значення другої похідної. Тобто:

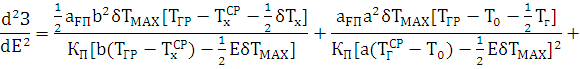
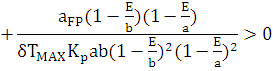
Розрахунковий вираз для визначення оптимального ступеня регенерації тепла Е_ОПТ буде мати вигляд:

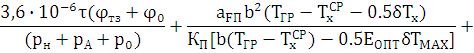
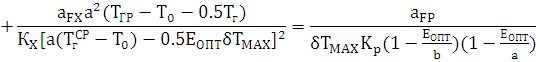
Просте рішення цього рівняння Е_ОПТ має труднощі. Разом з тим відомо, що значення Е_ОПТ повинно знаходитись в межах від 0 до 1.

Це рівняння може бути вирішено одним з чисельних методів вирішення трансцендентних рівнянь на ЕОМ (наприклад методом половинного розподілу).

3. Алгоритм вирішення трансцендентного рівняння методом половинного розподілу відносно ступеня регенерації теплоти

Нехай функція f(x), буде екстремальною на проміжку [a,b] (тобто, на цьому інтервалі вона має єдиний екстремум – максимум або мінімум), х – точка мінімуму; - точність. [4]

Оберемо достатньо мале та підрахуємо х₁ та х₂:

Потім обчислюємо значення функцій:

якщо f(x₁)<F(x₂), то а₁=а , b₁=x;

якщо f(x₁)>F(x₂), то а₁=x , b₁=b;

Відомо, що точка х* знаходиться на проміжку [a₁,b₁] при обчисленні х₃ та х₄порівнюючи їх.

При цьому неточність визначення x_n:

При цьому неточність визначення Х_n:

Рис1. Метод половинного розподілу.

Особливість розрахунку коефіцієнта тепловіддачі від киплячої води до стінки труби (конвективну складову не враховуємо) полягає в тім, що він залежить від поверхневої густини теплового потоку α₂=α₂(q) і отже, розрахунок α₂ носить ітераційний характер. У даному розрахунку рекомендується застосувати один з методів послідовного наближення – метод половинного розподілу. Принцип дії цього методу пояснимо за допомогою Рис2.

Рис2. Пошук значення q методом половинного розподілу

На початку задамося двома значеннями q: q₁ і q_2, причому таким чином, щоб охопити всю область можливих значеньqу теплообміннику. Цим значенням q₁іq₂будуть відповідати деякі температурні напори ∆t₁ і∆t₂. Після цього при q= 0,5(q₁+q₂) визначаємо α₂, К, ∆tі порівнюємо отримане значення ∆tз вихідним ∆t^ИСX. У випадку ∆t>∆t_ИСХ (як показано на мал.) приймаємо значення q₂^’ ( – друга ітерація), рівним q, тобто зважуємо область пошуку вдвічі, і знову повторюємо розрахунок при .

Припустимо, що знову отримане значення ∆t^’ < ∆t_ИСХ(див. мал.), тоді зменшення області вдвічі здійснюється переміщенням лівої границі q₁^’’ = q^’. Процес половинногопродовжується доти, поки не буде досягнута задана точність перебування ∆t_ИСХ