1. Обробка даних з застосуванням регресійних моделей

На поведінку складних технічних об’єктів мають вплив різні параметри, частина з яких носять випадковий характер. Для оцінки їх значимості на об’єкті, що вивчається, необхідно провести низку дослідів, змінюючи обрані управляючі параметри (фактори), і фіксуючи за показниками вимірювальних приладів значення характеристик об’єкта (відгуки), що цікавлять. Сукупність вхідних і вихідних параметрів називається експериментом і представляється зазвичай у вигляді наступної таблиці:

Таблиця 1.1 ‑ Дані n спостережень

Дослід	Значення факторів						Відгуки
k	x1	x2	. . .	xi	. . .	xm	y
1	x11	x21	. . .	xi1	. . .	xm1	y1
2	x12	x22	. . .	xi2	. . .	xm2	y2
. . .				. . .
k	x1k	x2k	. . .	xik	. . .	xmk	yk
. . .
n	x1n	x2n	. . .	xin	. . .	xmn	yn

Тут x₁, x₂,…, x_m – обрані фактори; y – спостережувана величина; x_ik – експериментальне значення фактора i в досліді k; y₁, y₂,…, y_n – значення отриманих відгуків.

При опрацюванні експериментальних даних виникає необхідність визначити математичну залежність характеристики об’єкту, що цікавить, від обраних факторів. При цьому необхідно мати на увазі, що дослідні дані можуть мати похибки, часом досить істотні. Таку залежність прийнято називати регресійною моделлю або рівнянням регресії, а методи, що дозволяють отримати цю залежність, прийнято називати методами регресійного аналізу.

Зазвичай використовують регресійні моделі з постійними коефіцієнтами наступного вигляду:

, (1.1)

де – спостережувана величина, розрахована за моделлю; f₁; f₂;…, f_N – обрані функції моделі; a₁; a₂;…, a_N – шукані коефіцієнти моделі.

За відсутності фізичних міркувань в якості функцій f використовують поліноми першого або другого порядку, наприклад:

(1.2)

Це лінійна модель першого порядку з постійними коефіцієнтами a₀, a₁, a₂, що визначає залежність величини від двох факторів x₁ і x₂.

З метою обліку нелінійних властивостей об’єкта в неї необхідно включити фактори в другій ступені, отримуючи модель другого порядку:

(1.3)

При обробці даних експерименту буває можливим виділити вплив на спостережувану величину тільки одного визначального фактора. В такому випадку рівняння регресії (1.1) спрощується і приймає наступний вигляд:

, (1.4)

де x – визначальний фактор; f₁; f₂;…, f_N – обрані функції моделі; a₁; a₂;…, a_N – шукані коефіцієнти моделі.

В однофакторних моделях широко застосовують різні математичні функції: поліноміальні, експоненціальні, логарифмічні, тригонометричні і інші. Вибір таких функцій залежить від особливостей об’єкту, що вивчається, також досвіду і інтуїції дослідника.

Для знаходження коефіцієнтів моделі зазвичай використовують критерій найменших квадратів:

(1.5)

Мінімум цієї функції можливо знайти, використовуючи умову екстремуму функції декількох змінних:

(1.6)

В результаті виходить система лінійних алгебраїчних рівнянь відносно невідомих коефіцієнтів моделі a. Вона може бути вирішена одним з чисельних методів лінійної алгебри, наприклад методом виключення Гауса.

Інформація, що дозволяє за даними експерименту одразу обрати відповідний вид регресійної моделі, часто відсутня. Це приводить до необхідності перебору різних функцій моделі і вибору найкращої з них. Щоб оцінити адекватність отриманої моделі розроблені спеціальні статистичні процедури. Оскільки вони достатньо складні і вимагають виконання великого об'єму обчислень, то на практиці часто застосовують спрощений підхід, заснований на виборі найкращої моделі за яким-небудь одним показником. В якості такого показника, що відображує міру якості регресійної моделі, часто розглядають коефіцієнт детермінації. Коефіцієнт детермінації показує, яка доля варіації змінної y, що пояснюється, врахована в моделі і обумовлена впливом на неї факторів, включених в модель:

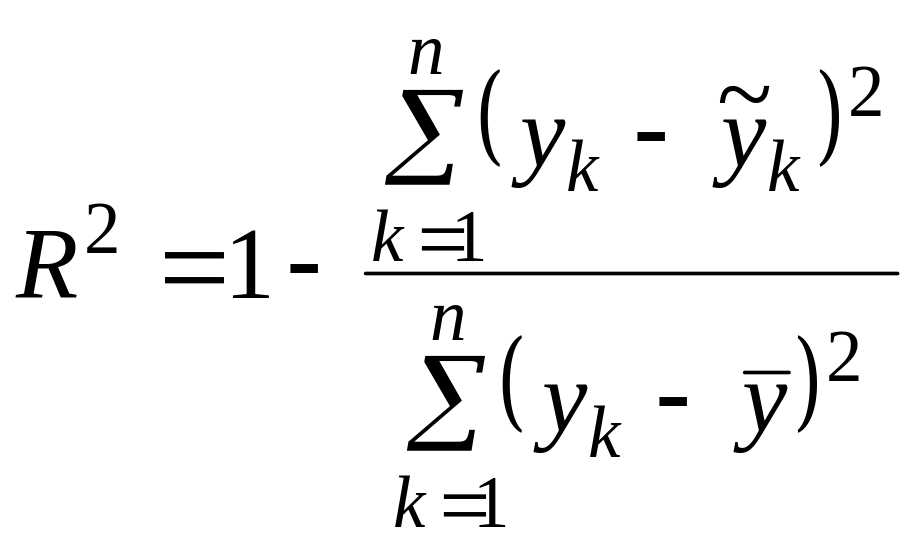(1.7)

де y_k – дослідні значення величини, що спостерігається, – середнє значення величини, – значення величини, розраховані за моделлю.

Чим ближче коефіцієнт детермінації R² до 1, тим вище якість моделі. Достатньо якісною можливо признати модель з коефіцієнтом детермінації вище 0,8.