
- •Методичні вказівки
- •Методичні вказівки
- •1 Загальна характеристика метода, що застосовується
- •2 Завдання для виконання роботи
- •3. Вимоги до звіту
- •4. Контрольні питання
- •1. Обробка даних з застосуванням регресійних моделей
- •2. Застосування засобів Mathcad для обробки експериментальних даних
- •3. Завдання для виконання роботи
- •4. Вимоги до звіту
- •5. Контрольні питання
- •Лабораторна робота №3
- •1. Загальна характеристика методу, що застосовується
- •2. Застосування теоретичного методу для дослідження енергетичного агрегату
- •3. Рішення задачі чисельним методом
- •4. Завдання для виконання роботи
- •5. Вимоги до звіту
- •6. Контрольні питання
- •1. Загальна характеристика теплообмінника
- •2. Математична модель
- •3. Метод рішення
- •4. Завдання для самостійного розрахунку
- •5. Вимоги до звіту
- •6. Контрольні питання
- •1. Загальна характеристика емпіричного і аналітичного методів дослідження
- •2. Застосування емпіричного і аналітичного методів для дослідження теплового процесу
- •3. Завдання для самостійного розрахунку
- •4. Вимоги до звіту
- •5. Контрольні питання
2. Застосування емпіричного і аналітичного методів для дослідження теплового процесу
Розглянемо достатньо простий технологічний процес охолодження стальних поковок в умовах ковальського цеха машинобудівного заводу. Поковки мають діаметр від 250 до 900 мм і виконані з вуглецевої і середньолегованої сталі. Залежно від кінцевого призначення поковки нагріті до температури від 1000оС до 1260оС. Процес охолодження поковок відбувається на відкритому повітрі на протязі від 3 до 32 хвилин. За умовами виробництва необхідний прогноз температури поверхні поковок залежно від часу охолодження.
Для вивчення цього процесу були проведені вимірювання температури поверхні великого числа поковок через різні проміжки часу. Після обробки експериментальних даних була отримана наступна емпірична залежність:
![]() , (2.1)
, (2.1)
де Tп – температура поверхні поковки, oC; Tс – температура навколишнього середовища, oC; T0 – початкова температура поковки, oC; – час процесу, хвилин; R – радіус поковки, м.
С метою застосування аналітичного методу дослідження розглянемо основні процесі, що відбуваються при охолодженні поковок. Так як охолодження відбувається на відкритому повітрі, то тепло передається в навколишнє середовище випромінюванням і конвекцією. При цьому температура навколишнього середовища залишається постійною. Через те, що обдув і інші засоби інтенсифікації охолодження не застосовуються, то має місце вільна конвекція. Приймаємо припущення, що поковка рівномірно охолоджується по периметру і довжині. Так як формування температурного стану поковок перед процесом охолодження включає різні технологічні процеси, то приймемо, що кожна поковка повністю прогріта до заданої початкової температури T0. Охолодження поверхні поковки приводить до теплопередачі всередині її об'єму. Цей процес визначається теплопровідністю, причому через малий час процесу теплофізичні властивості матеріалу поковок можна прийняти постійними.
Для аналітичного опису процесу охолодження поковок запишемо наступну математичну постановку задачі:
- диференційне рівняння теплопровідності в циліндричній системі координат
![]() , (2.2)
, (2.2)
- гранична умова на поверхні
![]() , (2.3)
, (2.3)
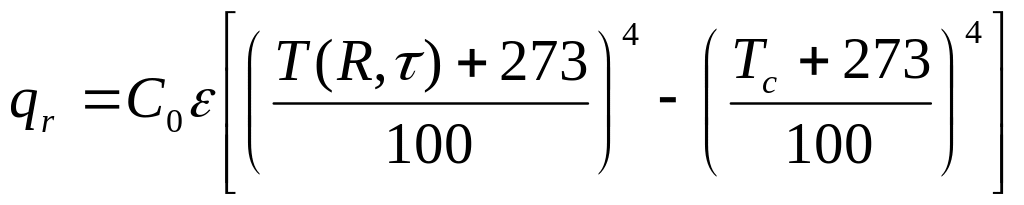 , (2.4)
, (2.4)
![]() , (2.5)
, (2.5)
- умова в центрі циліндра
![]() , (2.6)
, (2.6)
- початкова умова
![]() (2.7)
(2.7)
де
![]() – температура поковки, оС;
r
– радіальна координата, м;
– час, с; R
– радіус поковки, м; a
– температуропровідність матеріалу,
м2/c;
– теплопровідність матеріалу, Вт/(мК);
qr
і qk
– густина радіаційного і конвективного
теплових потоків на поверхню поковки,
Вт/м2;
С0
– приведений коефіцієнт випромінювання
чорного тіла, Вт/(м2К4);
– ступінь чорноти поверхні поковки;
– коефіцієнт тепловіддачі конвекцією,
Вт/(м2К);
Tc
– температура навколишнього середовища,
оС;
T0
– початкова температура поковки, оС.
– температура поковки, оС;
r
– радіальна координата, м;
– час, с; R
– радіус поковки, м; a
– температуропровідність матеріалу,
м2/c;
– теплопровідність матеріалу, Вт/(мК);
qr
і qk
– густина радіаційного і конвективного
теплових потоків на поверхню поковки,
Вт/м2;
С0
– приведений коефіцієнт випромінювання
чорного тіла, Вт/(м2К4);
– ступінь чорноти поверхні поковки;
– коефіцієнт тепловіддачі конвекцією,
Вт/(м2К);
Tc
– температура навколишнього середовища,
оС;
T0
– початкова температура поковки, оС.
Для находження зміни температури поверхні поковки в часі аналітичним методом необхідно вирішити поставлену математичну задачу, що визначається рівняннями (2.2) – (2.7). Радіаційний тепловий потік (2.4) залежить від значень температур в 4-й ступені, що робить задачу нелінійною. Тому для її рішення доцільно застосувати чисельний метод.
Розташовуємо
розрахункові вузли по радіусу поковки
з постійним кроком
![]() ,
де N
– загальне число вузлів. Координати
цих вузлів визначаються як
,
де N
– загальне число вузлів. Координати
цих вузлів визначаються як
![]() ,
де
,
де
![]() – номера вузлів. Так само вводимо вузлову
сітку по часу
– номера вузлів. Так само вводимо вузлову
сітку по часу
![]() ,
де
,
де
![]() – номер розрахункового кроку. Далі
переходимо від безперервної функції
температур
до дискретної
– номер розрахункового кроку. Далі
переходимо від безперервної функції
температур
до дискретної
![]() і апроксимуємо диференційне рівняння
теплопровідності (2.2) за допомогою явної
скінченно-різницевої схеми. При цьому
для підвищення точності розрахунку для
вузла N,
що розташований на поверхні поковки,
застосовуємо метод теплового балансу.
і апроксимуємо диференційне рівняння
теплопровідності (2.2) за допомогою явної
скінченно-різницевої схеми. При цьому
для підвищення точності розрахунку для
вузла N,
що розташований на поверхні поковки,
застосовуємо метод теплового балансу.
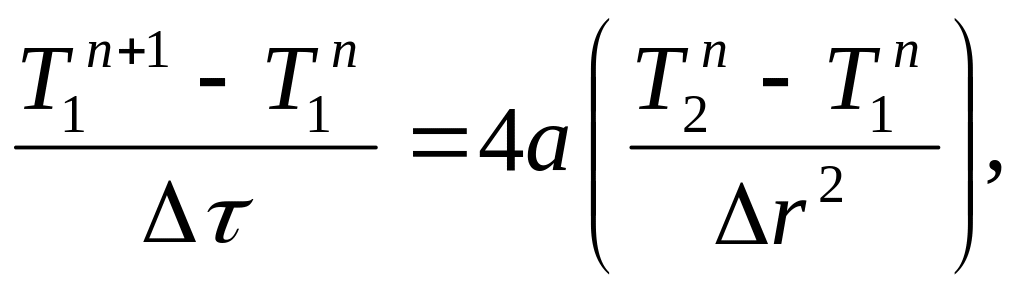 (2.8)
(2.8)
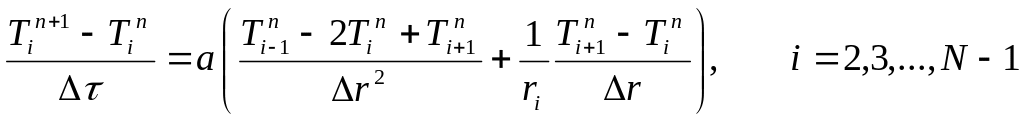 , (2.9)
, (2.9)
![]() (2.10)
(2.10)
де
і C
– густина і теплоємність матеріалу;
![]() – величина виділеного об'єму для вузла
N;
– величина виділеного об'єму для вузла
N;
![]() і
і
![]() – внутрішня і зовнішня поверхня об'єму
N.
– внутрішня і зовнішня поверхня об'єму
N.
Розрахункові формули для знаходження температур у вузлах приймуть вигляд:
![]() , (2.11)
, (2.11)
![]() , (2.12)
, (2.12)
![]() , (2.13)
, (2.13)
де
![]() – сітковий критерій Фур’є.
– сітковий критерій Фур’є.
Для
забезпечення стійкості явної схеми
повинна виконуватися умова
![]() .
Це накладає обмеження на крок розрахунку
за часом
.
Це накладає обмеження на крок розрахунку
за часом
![]() .
.
