4. Розрахунок робочих характеристик
За робочі
характеристики маємо залежності фазного
струму статора Is,
ККД ,
коефіцієнта потужності cos,
вхідної потужності
,
ковзанняs
і частоти обертання ротора n
від корисної (вихідної) потужності Р.
Щоб отримати ці характеристики, задаємо різні значення потужності Р, які вказані в табл. 3.1 у відносної формі
,
і
проводимо розрахунки
за методикою, яка використовується для
визначення параметрів номінального
режиму роботи. При цьому замість
номінальних значень потужності
,
фазного струму обмотки статораIsN,
ККД
,
коефіцієнта потужності cosN
, ковзання sN,
частоти
обертання nN
тощо треба оперувати з їхніми поточними
значеннями, виключаючи індекс N,
тобто це Р,
Is,
,
cos,
s,
n
тощо.
У перший стовпчик при Р
=
0 вносяться дані режиму неробочого ходу.
Результати
основних етапів розрахунку механічних
характеристик викладені в табл. 3.1. За
цими результатами будуємо залежності
Is(Р),
(Р),
cos(Р),
(Р),
s(Р),
n(Р).
Таблиця 3.1 – Розрахункові дані для побудови робочих характеристик асинхронного двигуна
|
Параметри |
Корисна
потужність
| |||||
|
0 |
0,1 |
0,5 |
0,75 |
1 |
1,25 | |
|
P, кВт |
0 |
0,15 |
0,75 |
1,125 |
1,5 |
1,875 |
|
s, в.о. |
0,002 |
0,048 |
0,25 |
0,398 |
0,569 |
0,776 |
|
cos |
0,1223 |
0,22 |
0,55 |
0,68 |
0,78 |
0,81 |
|
Is |
0,2208 |
0,225 |
0,27 |
0,319 |
0,376 |
0,464 |
|
Рin, Вт |
0,0358 |
0,067 |
0,199 |
0,291 |
0,393 |
0,509 |
|
|
0 |
0,449 |
0,752 |
0,772 |
0,763 |
0,736 |
,
в.о.
За даними таблиці 3.1 будуємо робочі характеристики, що приведені на рис. 3.6.
Рисунок 3.6 – Робочі характеристики асинхронного двигуна
4.1 Розрахунок максимального обертального моменту
Для розрахунку максимального моменту використовується перетворена схема заміщення асинхронного двигуна (рис.3.5), у якої для опору Rl треба взяти значення RMmax, яке відповідає роботі двигуна в режимі максимального моменту. Індуктивні опори визначаються з урахуванням насичення, яке відповідає навантаженню двигуна при максимальному моменті.
Розрахунок максимального моменту проводиться за умови використання напівзакритих трапецеїдальних пазів статора і овальних напівзакритих пазів ротора.
4.1.1 Змінна частина коефіцієнта провідності пазового розсіяння статора
|
|
|
(3.24) |
,
де
− коефіцієнт, що враховує укорочення
кроку обмотки статора, обирається за
[4],
.
Підставляємо отримані значення у (3.14)
.
4.1.2 Складова коефіцієнта провідності розсіяння обмотки статора, залежна від насичення
,
4.1.3 Змінна частина коефіцієнта пазового розсіяння обмотки ротора у випадку напівзакритого паза овальної форми
.
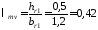4.1.4 Складова коефіцієнта провідності розсіяння обмотки ротора, залежна від насичення
,
4.1.5 Індуктивний опір розсіяння двигуна, залежний від насичення, Ом,
,
де
,
– коефіцієнти провідності розсіяння
статора і ротора.
4.1.6 Індуктивний опір розсіяння двигуна, незалежний від насичення, Ом,
.
4.1.7 Струм ротора при максимальному моменті, А,
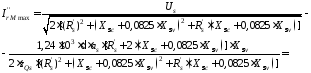
4.1.8 Повний опір схеми заміщення при максимальному моменті, Ом,
.
4.1.9 Повний опір схеми заміщення при нескінченно великому ковзанні, Ом,
.
4.1.10 Еквівалентний опір схеми заміщення при максимальному моменті, Ом,
.
4.1.11 Кратність максимального моменту
.
4.1.12 Критичне ковзання при максимальному моменті
.
4.2 Розрахунок початкових пускових струму і обертального моменту
При визначенні пускових струму і обертального моменту враховується явище витіснення струму в пазах короткозамкненої обмотки ротора і насичення зубців статора і ротора на шляхах потоків розсіяння в них.
4.2.1 Активні і індуктивні опори двигуна в режимі пуску.
4.2.1.1 Висота стрижня клітки ротора, мм,
.
4.2.1.2 Зведена висота стрижня ротора для литої алюмінієвої клітки
.
4.2.1.3 Розрахункова глибина проникнення струму в стрижні, мм,
|
|
|
(3.25) |
,де kRa − коефіцієнт активного опору, обирається за [4], kRa = 0,05.
Підставляємо отримані значення у (3.25)
.
4.2.1.4 Ширина стрижня на розрахунковій глибині проникнення струму, мм,
,
4.2.1.5 Площа поперечного перерізу стрижня при розрахунковій глибині проникнення, мм2,
.
4.2.1.6 Коефіцієнт витіснення струму
,
де
–
площа поперечного перерізу стрижня
ротора без урахування витіснення
струму.
4.2.1.7 Активний опір стрижня при 20С для пускового режиму, Ом,
.
4.2.1.8 Активний опір обмотки ротора при 20С, зведений до обмотки статора, для пускового режиму, Ом
,
де
= 21733–
коефіцієнт зведення.
4.2.1.9 Коефіцієнт провідності розсіяння паза ротора при пуску для овального напівзакритого паза (рис.3.1)
|
|
|
(3.26) |
,
де
− коефіцієнт індуктивного опору,
обирається за [4],
= 0,98.
Підставляємо отримані значення у (3.26)
.
4.2.1.10 Коефіцієнт провідності розсіяння обмотки ротора при пуску
.
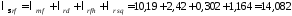4.2.1.11 Індуктивний опір розсіяння двигуна при пуску, залежний і не залежний від насичення, Ом,
;
.
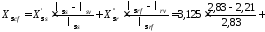
4.2.1.12 Активний опір двигуна при пуску, Ом,
.
4.2.2 Початкові пускові струм і момент двигуна.
4.2.2.1 Струм ротора при пуску, А,
.
4.2.2.2 Повний опір схеми заміщення при пуску, Ом,
.
4.2.2.3 Індуктивний опір схеми заміщення при пуску, Ом,
.
4.2.2.4 Активна складова струму статора при пуску, А,
.
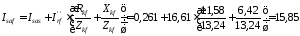4.2.2.5 Реактивна складова струму статора при пуску, А,
.
4.2.2.6 Фазний струм статора при пуску, А,
.
4.2.2.7 Кратність початкового пускового струму
.
4.2.2.8 Активний опір ротора при пуску, зведений до статора, при розрахунковій робочій температурі, Ом
.
4.2.2.9
Кратність початкового пускового
обертального моменту (
, кВт)
.
За
результатами розрахунку пункту 3.4.7.2
будуємо механічну характеристику
трифазного асинхронного двигуна (рис.
3.7)
