Степенная функция Показательная функция Логарифмическая функция Тригонометрические функции Обратные тригонометрические функции

Элементы теории поля

Скалярное поле определяется скалярной функцией точки , где  – точка пространства.  Векторное поле определяется векторной функцией точки , где M – точка пространства и  – радиус-вектор точки M. В координатной форме , где функции  – проекции вектора  на координатные оси.  Оператор Гамильтона (набла) – . Вектор  называется градиентом поля  в данной точке . Если направление задано вектором , то производная функции  по направлению  находится по формуле:   – направляющие косинусы вектора . Дивергенцией (или расхождением) векторного поля  называется скаляр . Вихрем (ротором) векторного поля  называется вектор . Потоком векторного поля  через поверхность , определяемую единичным вектором нормали  к поверхности , называется поверхностный интеграл второго рода:  . Если  – замкнутая гладкая поверхность, ограничивающая объем V, и функции  непрерывны вместе со своими частными производными первого порядка в замкнутой области V, то имеет место формула Остроградского–Гаусса:  . Формула Остроградского-Гаусса в векторной форме: . Циркуляция векторного поля по произвольному замкнутому контуру L равна криволинейному интегралу второго рода (линейному интегралу) от вектора : . Если функции  непрерывно дифференцируемы и L – замкнутый контур, ограничивающий поверхность , то имеет место формула Стокса:  . Формула Стокса в векторной форме: .

Специальные виды векторных полей

Векторное поле  называется потенциальным, если вектор поля  является градиентом некоторой скалярной функции . Необходимым и достаточным условием потенциальности векторного поля  является равенство нулевому вектору вихря этого поля: . Векторное поле  называется соленоидальным, если .Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется дифференциальное уравнение первого порядка вида  или .

№1

Решить уравнение . В частности, найти решение, удовлетворяющее начальному условию . Учитывая, что  и вынося за скобки , получим , или, что то же самое, . Разделив обе части уравнения на произведение  получим: . Интегрируем обе части последнего равенства: . Учитываем то, что  и сокращаем обе части равенства на . Произвольную постоянную  удобно представить в виде . Тогда , откуда и получаем ответ . Для того, чтобы найти постоянную , учтем заданное условие : . Следовательно, искомое частное решение есть .

№2

Решить уравнение . Перепишем данное уравнение в таком виде: . Заменяя  на , получим: . Далее, разделяем переменные: . Интегрируя обе части последнего равенства, получаем: . Так как , то . Для удобства записи заменим , тогда , или, что то же самое, .

№3

Решить уравнение  при заданном начальном условии . Разделим переменные: . Интегрируем полученное равенство:  . Учитывая , получим . Так как по условию задачи . Подставляя , получим ответ: 

№4

Решить уравнение , если известно, что . Учитывая , получим . Интегрируем последнее равенство:  . Так как , то . Для более короткой записи результата, представим произвольную постоянную  в виде  и применим формулу суммы логарифмов к правой части равенства: . Из последнего равенства получаем: . Так как , то . Подставляя , получим .

Частные случаи дифференциальных уравнений второго порядка

Если дифференциальное уравнение имеет вид , т.е не содержит явным образом , то делается замена . Если дифференциальное уравнение имеет вид , т.е не содержит явным образом , то делается замена .

№1

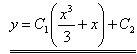Решить уравнение , если . Данное дифференциальное уравнение второго порядка не содержит явным образом , поэтому делаем замену  (полагая функцией от ), . Имеем:  . Учтем  и разделим переменные в последнем уравнении:. Интегрируя последнее равенство получаем: . Учитывая  результат интегрирования будет таким: . Отсюда следует . Так как , то , . Так как согласно начальным условиям при  и , то, учитывая  и  получим: . Подставляя найденные значения  получим ответ: 

№2

Решить уравнение  Данное дифференциальное уравнение второго порядка не содержит явным образом , поэтому делаем замену  (полагая функцией от ), . Имеем:  . Получили однородное уравнение, решаемое заменой . Тогда:  . Разделяем переменные и интегрируем: , откуда находим . Далее, так как  и , то . Возвращаемся к первоначальной замене . Применяя метод интегрирования по частям, найдем .

№3

Решить уравнение . если .. Данное уравнение не содержит явным образом переменной x, поэтому делаем замену . (полагая .функцией от ). Соответственно, . Подставляя эти замены в исходное уравнение, получим: . Вынося за скобки, получаем:  , откуда следует, что  или . Рассматривая первый случай () находим, что . Уравнение  преобразуем в таком виде: . Полученное уравнение первой степени – линейное. Делаем замену , где  - неизвестные функции переменной . Применяем метод Бернулли:  . Функцию  подбираем таким образом, чтобы было выполнено условие . Учитывая  разделим переменные в последнем уравнении: . Интегрируем последнее равенство:. Подставляя  в уравнение  и принимая во внимание  получим . Из последнего равенства следует . Применяя метод интегрирования по частям в интеграле  получим значение функции  в таком виде: . Так как  и , то . Так как согласно первоначальной замене , то . В условии задачи указаны начальные условия ( при ), которые представляется возможным применить с целью выяснения значения постоянной .. Подставляя ., получим ., откуда следует .. Учтем . и перепишем уравнение . в виде .. Далее, так как ., то из . следует .. Интегрируя это равенство, получаем .. Учитывая начальные условия найдем .. Тогда .

Применение криволинейных интегралов первого рода

Применение в геометрии

Пусть в плоскости Oxy задана кривая AB, и на этой кривой определена функция . 1. Площадь цилиндрической поверхности, определенной функцией , определяют по формуле . 2. Длину кривой AB определяют по формуле .

Применение в механике

Пусть дана материальная кривая L, плотность на которой меняется по формуле . 1. Масса кривой:  . 2. Статические моменты кривой относительно осей Ox и Oy:

3. Координаты центра тяжести :

4. Моменты инерции кривой относительно осей Ox, Oy и начала координат:

Примечание: 1. Если кривая задана в декартовой системе координат уравнением , то . 2. Если кривая задана уравнениями , или, для трехмерного пространства, . 3. Если кривая задана в полярной системе координат уравнением , то .Применение двойного интеграла

Применение в геометрии

1. Площадь ограниченной замкнутой области D в плоскости Oxy: 

2. Объем цилиндрического тела (образующие параллельны оси Oz), ограниченного снизу областью D плоскости Oxy, а сверху поверхностью 

3. Если участок поверхности, заданной уравнением  проектируется в область D на плоскости Oxy, причем функции  непрерывны в этой области, то площадь данного участка поверхности:

Применение в механике

Пусть на плоскости Oxy находится материальная пластина, имеющая форму ограниченной замкнутой области D, причем в каждой точке данной области плотность определяется непрерывной функцией  1. Масса пластины:  2. Статические моменты пластины относительно осей Ox и Oy:

3. Координаты центра тяжести 

4. Моменты инерции пластины относительно осей Ox, Oy и начала координат:

Формула Ньютона — Лейбница

Пусть дана кривая , соединяющая две точки  и  (одномерная цепь) в многообразии произвольной размерности. Форма  нулевой степени класса  — это дифференцируемая функция . Формула Стокса тогда записывается в виде

[править]Теорема Грина

Пусть  — плоскость, а  — некоторая её ограниченная область с кусочно-гладкой жордановой границей. Форма первой степени, записанная в координатах  и  — это выражение, и для интеграла этой формы по границе области  верно

Формула Остроградского

Пусть теперь  — кусочно-гладкая гиперповерхность (), ограничивающая некоторую область  в -мерном пространстве. Тогда интеграл дивергенции поля по области равен потоку поля через границу области :

Что эквивалентно записи:

или

Формула Кельвина — Стокса

Пусть  — кусочно-гладкая поверхность () в трёхмерном евклидовом пространстве (),  — дифференцируемое векторное поле. Тогда циркуляция векторного полявдоль замкнутого контура  равна потоку ротора (вихря) поля через поверхность , ограниченную контуром:

или в координатной записи:

Связь с производной по направлению

Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции  по направлению  равняется скалярному произведению градиента  на единичный вектор :

Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.

[править]Градиент в ортогональных криволинейных координатах

где  — коэффициенты Ламе.

[править]Полярные координаты (на плоскости)

Коэффициенты Ламе:

Отсюда:

[править]Цилиндрические координаты

Коэффициенты Ламе:

Отсюда:

[править]Сферические координаты

Коэффициенты Ламе:

.

Отсюда: