1 Теңдеулер және теңдеулер жүйесін оқыту
1.1 Теңдеулер және теңдеулер жүйесі ұғымы
Математиканы оқытудың білімдік мақсаты – барлық оқушыларды математиканың ғылыми негіздері туралы жүйелі біліммен және оларды толық, сапалы да берік игеруге қажетті біліктіліктермен, дағдылармен қаруландыру болып табылады. Осындай білім алу нәтижесінде оқушылардың ақыл-ойы дамиды, деңгейі кеңиді. Математиканың негізгі мазмұнын құрайтын оқыту материалдарынбіріктіретін, үйлестіретін, оның ғылымилығы және қолданбалығы принциптерін іске асыруға мүмкіндік беретін негізгі ұғымдар–теңдеулер мен теңсіздіктер. Осы ұғымдармен байланысты шығарылатын есептер оқушылардың логикалық ойлау, кеңістікті елестету, жеке бас қабілеттерін дамытуға бірден-бір себепші болатын басты құрал.
Алған білімдерін дәстүрлі емес жағдайларда қолдана білуге, өмірлік жоспарларын іске асыруда, жоғары сынып оқушыларының сапалы білім алуында «Теңдеулер мен теңдеулер жүйесін шешу» тақырыбын оқып-үйрену өте маңызды орын алады.
Теңдік, теңдеулер және теңсіздіктер түсінігі ерте заманнан өмір және практика қажеттілігінен туындаған болатын.
Мысалы, осыдан 4000 жыл бұрын вавилондықтар геодезиялық, құрылыс салудың және әскери дайындық есептерін бірінші және екінші дәрежелі теңдеулер арқылы шығарған.
Осындай дәрежедегі теңдеулерді ежелгі Қытай мен Үнді ғалымдары да шығара білген. Теңдеулер арқылы шығарылатын есептер көне мәтіндерде кездеседі.
Ерте кезден бастап жер бөліктерінің ауданын табуға және әскери сипаттағы жер жұмыстарына, сонымен қатар астрономия және математиканың дамуына байланысты бірінші ғана емес, екінші дәрежелі теңдеулерді шешу қажеттілігі пайда болады.
Б.з.д. 2000 жыл бұрын вавилондықтардың қолжазбаларында толық емес квадрат теңдеулермен қатар
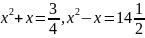
тәрізді толық квадрат теңдеулер де кездеседі.
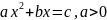(1)
түріне келтірілген квадрат теңдеулерді шешудің жалпы ережесін үндінің тағы бір ғалымы Брахмагупта (VIIғ.) берген (1) теңдеуінде a-дан басқа коэффициенттер теріс болуы мүмкін.
Теңдеулер және теңдеулер жүйесін қарастыру, оларды шешу мәселелері білімде және ғылымда кеңінен қарқынды қарастырыла бастады.Өйткені, осы тақырыптарды жақсы түсінген, саналы меңгерген оқушылар мектептік математика курсын сапалы және терең деңгейде оқып-үйрене алатын болады.
Мектеп курсында бұл тақырыптар жүйелі түрде екінші сыныптан бастап оқытылады, содан мектеп бітіргенше жалғастырылады. Сондықтан бұл тақырыптар мектеп математика курсы бойынша білім деңгейін тереңдетудің және оның сапасын жақсартудың негізгі арқауы және құралы болып табылады. Оған мына мысалдардан көз жеткізуімізге болады деп ойлаймын.
Теңдеулер
Көрсеткіштік
теңдеулер
Тригонометриялық
теңдеулер
Трасценденттік
теңдеулер
Алгебралық
теңдеулер
Иррационал
теңдеулер
Рационал
теңдеулер
Бөлшек-рационал
теңдеулер
Бүтін
теңдеулер
Жоғары
дәрежелі теңдеулер
Квадрат
теңдеулер
Сызықтық
теңдеулер
Логарифмдік
теңдеулер
Анықтама. Теңдеудің түбірі деп теңдеуді дұрыс теңдікке айналдыратын айнымалының мәнін айтады.
Теңдеуді шешу дегеніміз – оның барлық түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеп көрсету.
Теңдеулерді шешкенде мына қасиеттер қолданылады:
1) егер теңдеудегі қосылғыштың таңбасын өзгертіп, бір бөлігінен екінші бөлігіне көшірсе, онда берілген теңдеумен пара – пар теңдеу шығады;
2) егер теңдеудің екі бөлігін де нөлге тең емес бір ғана санға көбейтсе немесе бөлсе, онда берілген теңдеумен пара – пар теңдеу шығады.
Анықтама.
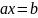түріндегі
теңдеуді, мұндағы
– айнымалы, a
мен b
– қандай да бір сандар,
бір
айнымалысы бар сызықтық теңдеу деп
атайды
Екі айнымалысы бар теңдеудің графигі
деп
координаталық жазықтықтың координаталары
осы теңдеудің шешімдері болып табылатын
барлық нүктелерінің жиынын айтады.
Анықтама. Екі айнымалысы бар теңдеулер жүйесінің шешімі деп жүйенің әрбір теңдеуін дұрыс теңдікке айналдыратын айнымалылар мәндерінің жұбын атайды.
Екі айнымалысы бар теңдеулер жүйелерін шешу
Ауыстыру тәсілі. Екі айнымалысы бар екі сызықтық теңдеу жүйесін ауыстыру тәсілімен шешкенде:
бір теңдеуден бір айнымалыны екіншісі арқылы өрнектейді;
бұл алынған өрнекті екінші теңдеудегі осы айнымалының орнына апарып қояды;
бұдан шыққан бір айнымалысы бар теңдеуді шешеді;
екінші айнымалының сәйкес мәнін табады.
Қосу тәсілі. Екі айнымалысы бар екі сызықтық теңдеу жүйесін қосу тәсілімен шешкенде:
айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болып шығатындай етіп, лайықты көбейткіштер таңдап алады да, жүйенің теңдеулерін сол көбейткіштерге көбейтеді;
алынған жүйе теңдеулерінің сол жақ және оң жақ бөліктерін мүшелеп қосады;
шыққан бір айнымалылы теңдеуді шешеді;
екінші айнымалының сәйкес мәнін табады.
Есептерді теңдеулер жүйесін құру арқылы шешу.
Теңдеулер жүйесін құру арқылы есептер шығарғанда қандай да бір белгісіз сандарды әріптермен белгілейді де, содан соң есептің артын пайдаланып, теңдеулер жүйесін құрады, бұл жүйені шешеді, шыққан нәтижені есептің шартына сәйкестендіріп түсіндіреді.