22

Лекция 9. Квантовые эффекты в нано-мдпт

Масштабирование требует сокращения как горизонтальных, так и вертикальных размеров МДПТ. Поэтому при уменьшении длины канала необходимо уменьшать толщины подзатворного окисла и обедненной области. Уменьшение толщины обедненной области требует увеличения концентрации примеси в подложке. В результате агрессивного масштабирования при переходе размеров в наноразмерную область толщина подзатворного окисла достигла 1нм, а концентрация примеси в подложке ~10¹⁸см^-3. Одновременно с уменьшением размеров растет электрическое поле в подзатворном диэлектрике и инверсионном слое. Наиболее очевидный квантовомеханический (КМ) эффект, связанный с очень тонким окислом, есть ток утечки вследствие прямого туннелирования через окисел. Экспоненциальный рост этого эффекта устанавливает минимальную практическую толщину окисла примерно 10Å. Вторым важным эффектом, играющим важную роль в работе наноразмерных МДП-транзисторов, является размерное квантование электронов в приповерхностном слое. Этот эффект оказывает влияние как на величину заряда, который может быть индуцирован в канале электродом затвора через окисел, так и на профиль распределения заряда в направлении, перпендикулярном поверхности. Размерное квантование может происходить не только в подложке, но и в поликремниевом затворе.

Влияние туннелирования рассмотрено в лекции, посвященной токам утечки в наноразмерном транзисторе. Оно проявляется не только в туннелировании через окисел, но и в туннелировании через обратно смещенный р-п переход сток-подложка при высокой концентрации примеси в подложке, а также вследствие GIDL-эффекта. В настоящей лекции будут рассмотрены проблемы размерного квантования в наноразмерных МДП-приборах.

9.1 Электрон в потенциальной яме

Когда электрон локализован в области, сравнимой с длиной волны электрона, начинают проявляться квантовомеханические эффекты.

Пусть электрон находится в бесконечно глубокой потенциальной яме, шириной L:

.

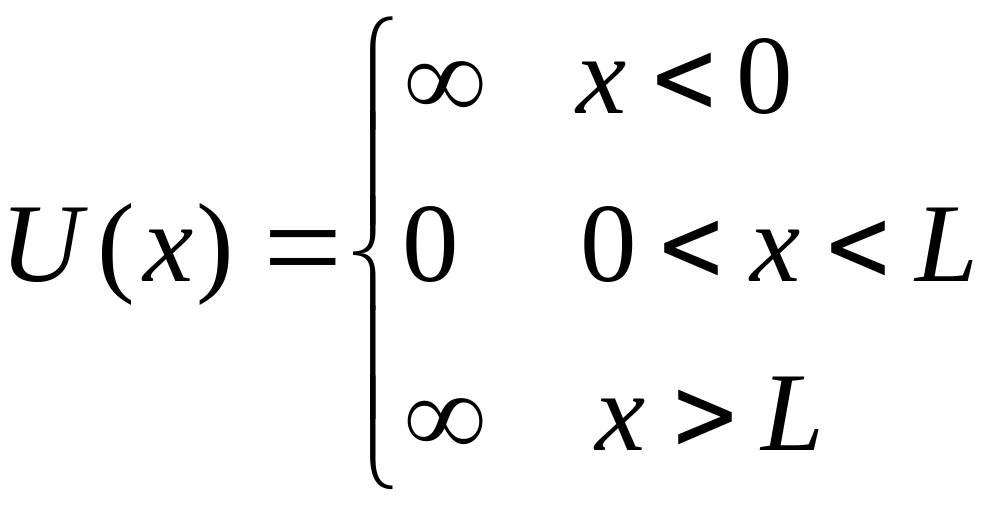Волновая функция электрона (в см^-1/2) удовлетворяет стационарному уравнению Шредингера

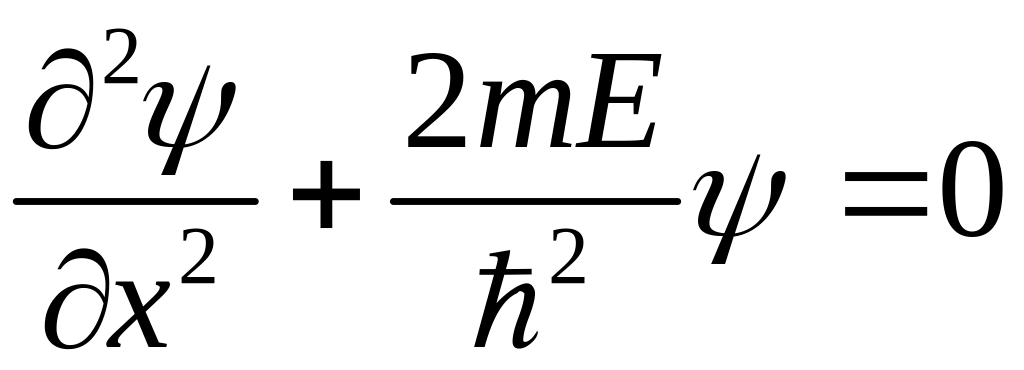
с граничными условиями . Решением уравнения является

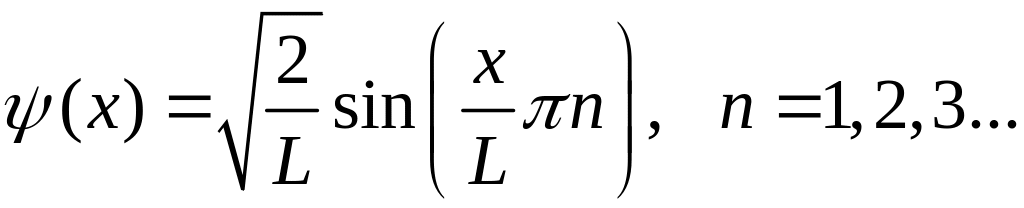
спектр разрешенных уровней энергии электрона E_n

,

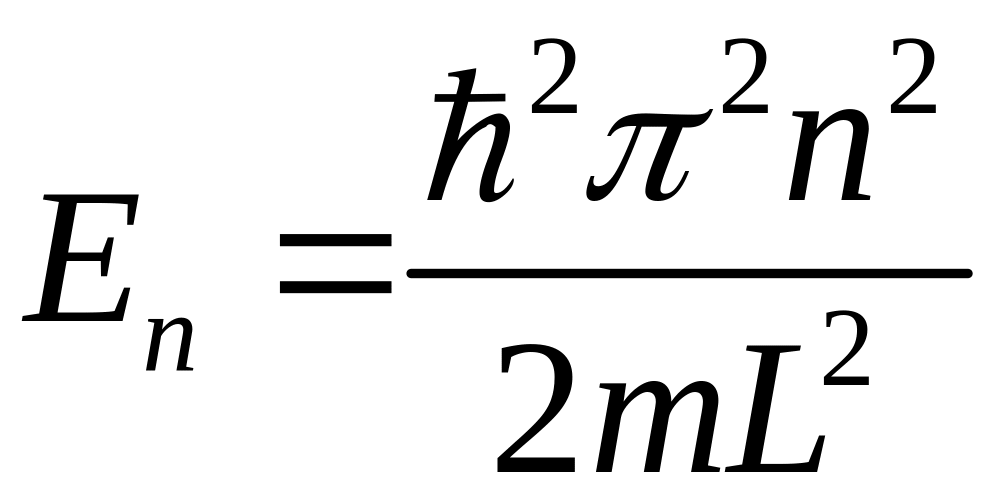а самый нижний уровень энергии ( ) определяется как

.

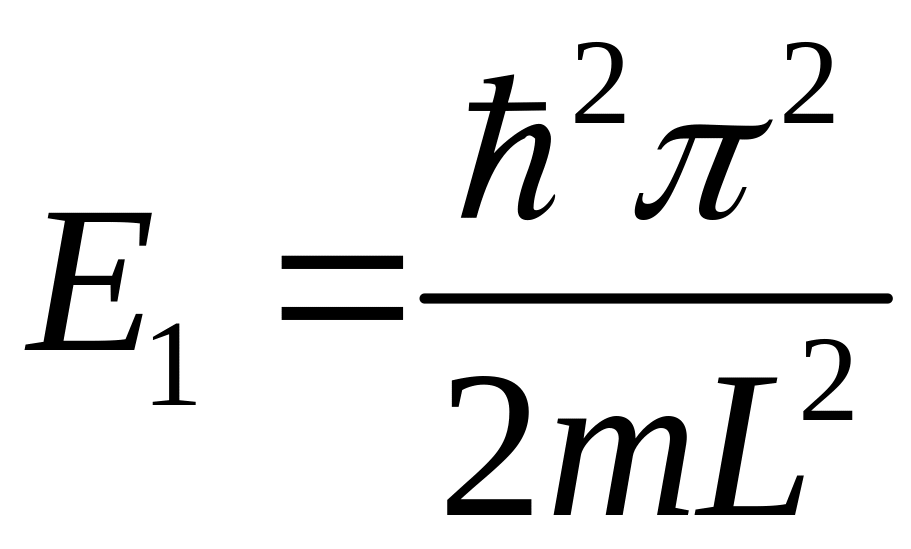В МДПТ в режиме инверсии электроны локализованы в потенциальной яме, а область локализации сравнима с длиной волны электрона. Поэтому становится необходимым учет КМ поведения электронов.

Полное решение для инверсного слоя кремния требует численного самосогласованного решения уравнений Пуассона и Шредингера. В подпороговом режиме, когда плотность инверсного заряда мала, можно считать, что изгиб зон определяется только зарядом обеднения. Тогда возможно развязать два уравнения и получить некоторое понимание влияния квантовомеханического эффекта (КМЭ) на пороговое напряжение. Так как электроны инверсного слоя локализованы в узкой области вблизи поверхности, где электрическое поле почти постоянно, хорошей аппроксимацией при рассмотрении потенциальной ямы является ее представление в виде бесконечно высокого барьера окисла для x < 0 и линейной зависимости потенциала вследствие заряда обеднения для x > 0 − приближение треугольной потенциальной ямы (triangular well approximation − TWA) (рис. 9.1).

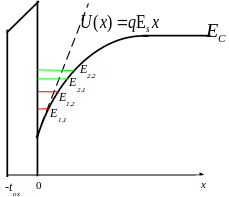
Рис.9.1 Треугольная потенциальная яма вблизи поверхности полупроводника.

Движение электрона ограничено только в направлении x, то есть перпендикулярно поверхности. В плоскости электрон движется как свободный электрон с эффективной массой . Волновую функцию электрона можно представить в виде суперпозиции волновой функции для электронов в плоскости

и волновой функции для движения перпендикулярно границе (по оси х) :

.

Волновая функция находится из решения уравнения Шредингера в приближении эффективной массы

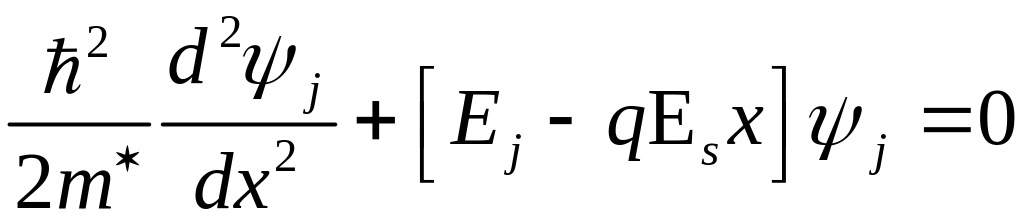(9.1.1)

Таким образом, при каждом значении электронный газ двумерен, то есть полностью описывается волновыми векторами и обладает квазинепрерывным спектром:

.

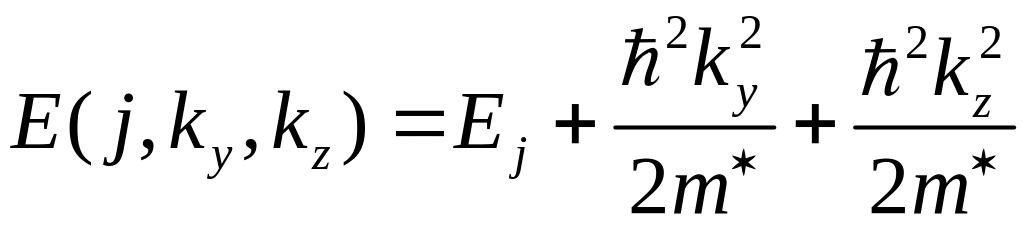Область энергий, которыми может обладать электрон с данным квантовым числом , называется поверхностной подзоной. В случае скалярной эффективной массы поверхностная подзона представляет собой параболоид вращения.

Уравнение Шредингера (9.1.1) решается при граничных условиях равенства нулю волновой функции при x = 0 и на бесконечности. Его решением являются функции Эйри (Airy)¹ , а собственные значения , находятся из условия [2]:

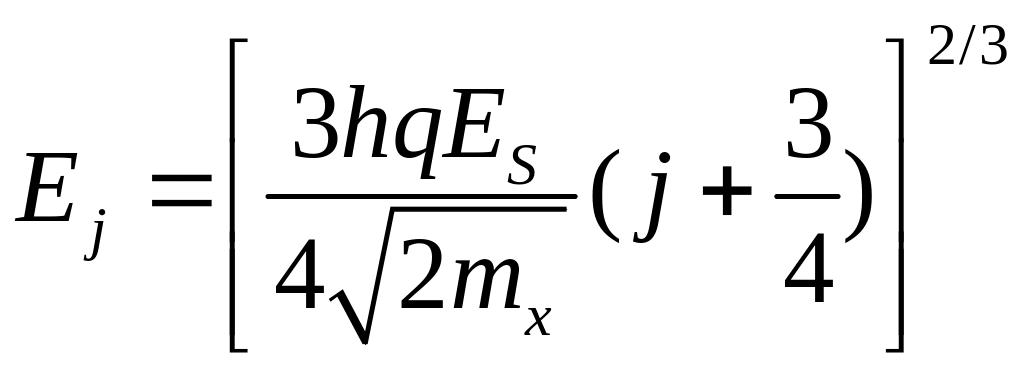, (9.1.2)

где − эффективная масса электрона в направлении ограничения (по оси x).

Эффективная масса электрона определяется зонной структурой кремния и ориентацией кристалла. Мы будем предполагать, что плоскость раздела Si-SiO₂ параллельна плоскости (100) решетки кремния. В этой плоскости изоэнергетические поверхности электронов имеют вид шести эллипсоидов, как показано на рис.9.2. Два из них ( ) вдоль оси ‹100› характеризуются продольной эффективной массой , а другие четыре ( ) вдоль той же оси ‹100› − поперечной эффективной массой . Энергетические уровни в этих двух типах долин

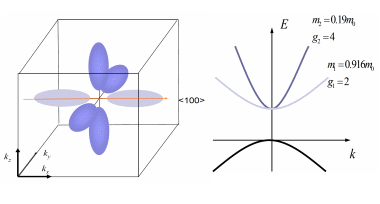Рис. 9.2

обозначаются как для первого типа долин (g₁) и для второго типа долин (g₂) и находятся из решения уравнений Шредингера с соответствующими эффективными массами:

.

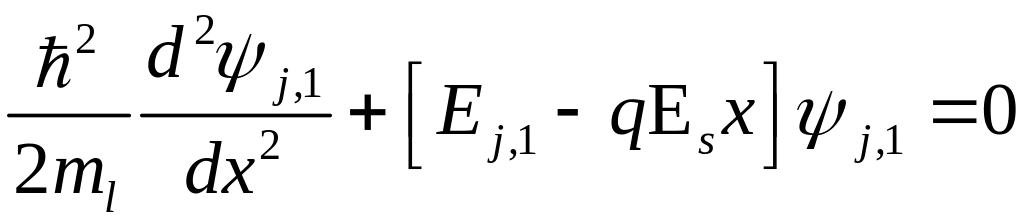
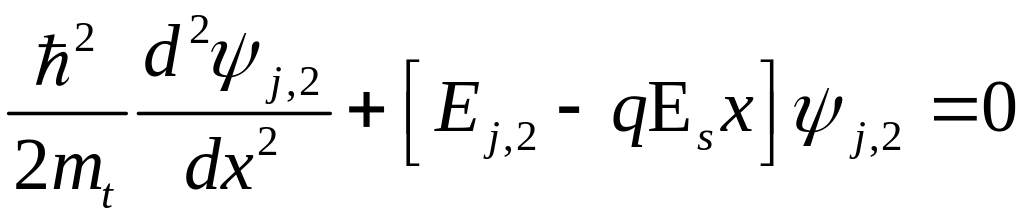Решение уравнений дает

,

.

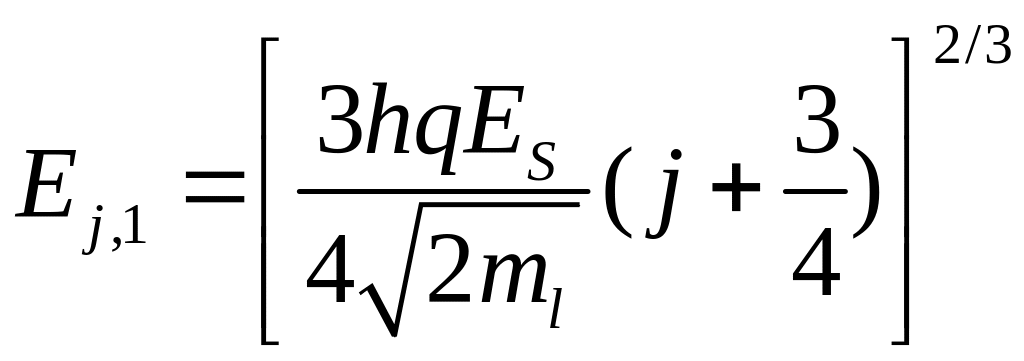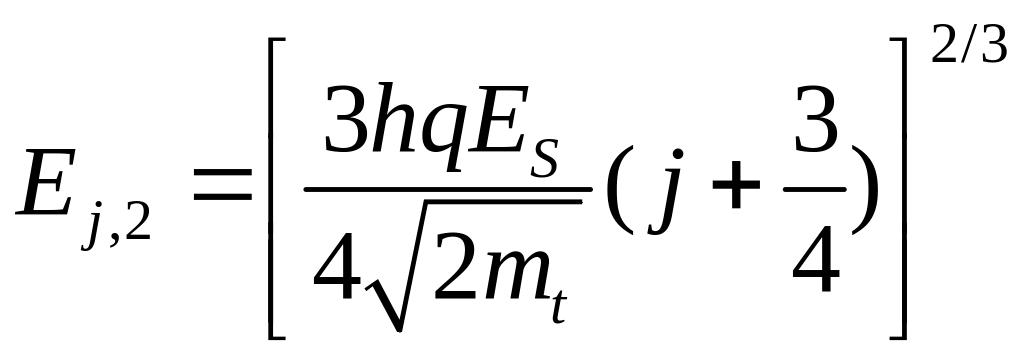Для энергетических уровней выполняется соотношение, , поскольку .

Зная решение уравнения Шредингера, можно найти среднее расстояние инверсного заряда (центроид) в j-той подзоне от поверхности кремния:

.

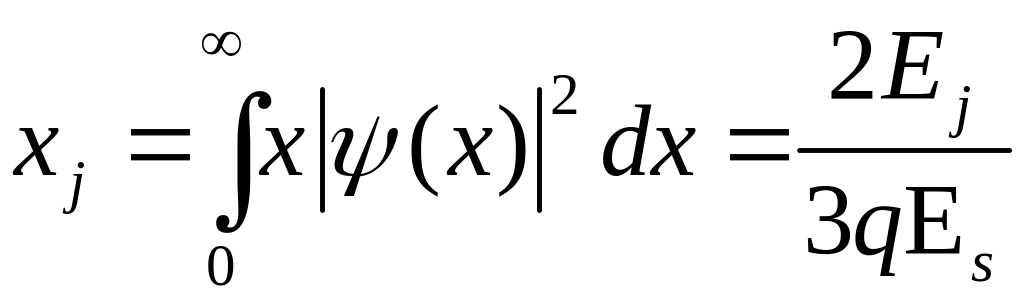Рис.9.3. Пример квантовомеханического расчета изгиба зон и энергетических уровней электронов инверсного слоя вблизи поверхности кремния. Основное состояние примерно на 40мэВ выше нижнего края зоны проводимости на поверхности. Пунктир – уровень Ферми при плотности электронов инверсного слоя 10¹²/см² [1].

На рис. 9.3 приведен пример расчета энергетических уровней и изгиба зон. Концентрация электронов имеет пик ниже границы кремний-оксид и равна нулю на границе, как диктуют граничные условия на волновую функцию. Это сильно отличается от классической модели, в которой пик концентрации электронов находится на поверхности, как показано на рис.9.4.

Квантовомеханическое поведение электронов инверсного слоя влияет на работу МДПТ двумя путями. Во-первых, в сильных полях пороговое напряжение становится выше, так как требуется больший изгиб зон, чтобы заселить самую нижнюю подзону при некоторой энергии выше дна зоны проводимости. Во-вторых, поскольку инверсный слой формируется ниже поверхности, он требует более высокого напряжения на затворе, чтобы создать данный уровень инверсной плотности заряда. В результате полупроводник ведет себя так, как если бы увеличилась ширина запрещенной зоны, величина которой зависит от поперечного поля и растет вместе с ним.

Рис.9.4. Классическое и квантовомеханическое распределения плотности электронов инверсного слоя - кремния. Пунктирная линия показывает распределение плотности электронов для самой нижней подзоны [1].

Увеличенная ширина запрещенной зоны делает более трудным для электронов переход из валентной зоны в зону проводимости, приводит к деградации собственной концентрации и увеличивает эффективный потенциал Ферми (расстояние от уровня Ферми до середины зоны). Теперь требуется больший изгиб зон, чтобы достичь необходимого уровня инверсии; это соответствует увеличению поверхностного потенциала на величину, которая изменяется с продольным электрическим полем. Это влияет на характеристики прибора и приводит к увеличению порогового напряжения в пМОПТ. Другими словами, эффективная толщина подзатворного оксида слегка больше, чем физическая толщина. Это уменьшает крутизну и рабочий ток МОПТ.