1.3 Размерность физической величины

Размерность ФВ – это выражение производной ФВ через основные ФВ в форме одночлена, составленного из произведения символов основных ФВ в различных степенях. Она показывает как производная величина связана с основными величинами.

Понятие размерности распространяется и на основные величины. Формула размерности основной величины совпадает с ее символом.

Размерность ФВ в соответствии с ИСО 31/0 следует обозначать знаком (от dimension).

Размерность основных физических величин в системе :

.

Размерность производной ФВ может быть найдена путем подстановки в правую часть определяющего уравнения вместо обозначений основных ФВ их размерностей. В определяющих формулах можно произвести замену величин на характерные величины, отбросить знаки математических операторов. При отбрасывании знаков математических операторов соблюдают следующее правило:

.

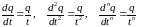Пример: Определяющее уравнение для скорости , размерность скорости .

Размерность любой производной механической величины в системе LMT может быть представлена следующим образом:

.

В системе СИ:

.

В этих формулах - показатели размерности физических величин, которые могут принимать различные значения: целые или дробные, положительные или отрицательные.

Широкое использование получили безразмерные величины.

Безразмерная физическая величина (безразмерная величина) – это ФВ, в размерность которой основные физические величины входят в степени, равной нулю.

Примеры безразмерных ФВ: КПД, относительная деформация, ... , т.е. любая величина, равная отношению двух однородных величин.

Безразмерными могут быть и иные комбинации размерных величин, например, т.н. критерии подобия.

Размерность единицы ФВ совпадает с размерностью самой ФВ.

Пользуясь размерностью величины, можно установить, во сколько раз изменится размер единицы данной производной ФВ при изменении размеров единиц величин, принятых за основные. Рассмотрим некоторую производную механическую величину, имеющую размерность:

.

Очевидно, что число раз , в которое возрастет или уменьшится размер новой единицы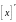 по сравнению с прежней единицей , выразится соотношением:

,

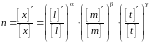где - прежние единицы длины, массы, времени;

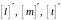- новые единицы тех же величин.

1.4 Практическое использование понятия «размерность» фв

1. Проверка правильности уравнений, полученных в ходе теоретических выводов: размерность правой и размерность левой частей равенства, связывающего различные ФВ, должны быть одинаковыми. В противном случае при выводе допущена ошибка или в уравнение входит неучтенный размерный коэффициент (см. приложение 2).

2. Установление функциональной связи между ФВ. Если число определяющих величин с независимыми размерностями равно числу основных единиц, то функциональная зависимость находится с точностью до постоянного множителя и имеет вид:

,

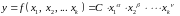где - неопределяемый коэффициент пропорциональности;

- определяющие величины с независимыми размерностями;

- число определяющих величин;

- показатели степени, подлежащие определению методом сравнения размерностей.

Примеры установления функциональных связей между физическими величинами приведены в приложении 4.

1.5 -теорема

Физические закономерности представляют собой функциональные зависимости между размерными величинами, характеризующими исследуемое явление. В соответствии с - теоремой всякое физическое соотношение между размерными величинами можно сформулировать как соотношение между безразмерными величинами.

Пусть зависимость

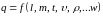(1.2)

отражает связь между размерной величиной 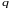и размерными независящими одна от другой величинами .

Будем полагать, что величины 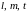являются основными в системе величин механики 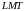и имеют независимые размерности (о независимости размерностей ФВ см. приложение 3).

Величины запишем в относительных единицах, т.е. в долях от некоторых характерных величин . Тогда зависимость (1.2) может быть представлена в относительном виде:

. (1.3)

Выразим производные характерные величины через основные характерные величины с помощью степенных одночленов:

, , , … . (1.4)

Основные характерные величины, в отличие от производных характерных величин, могут быть выбраны произвольно.

Пусть

. (1.5)

Тогда, с учетом (1.5), из (1.4) получаем:

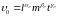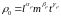, , ,… . (1.6)

Подставляя соотношения (1.5) и (1.6) в формулу (1.3), находим:

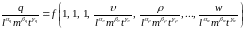(1.7)

Входящие в это выражение комплексы являются безразмерными. Обозначим указанные комплексы:

(1.8)

С учетом соотношений (1.8) выражение (1.7) можно представить следующим образом:

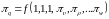
или в более компактном виде

.

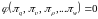Обобщение полученного результата на произвольное число величин, входящих в зависимость (1.2), приводит к -теореме:

функциональная зависимость между размерными величинами, из которых величин имеют независимые размерности, может быть представлена в виде связи между 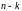безразмерными комплексами, каждый из которых является комбинацией из 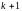размерной величины.

Эта теорема является основной в теории размерности. Следует заметить, что -теорема входит в число трех теорем теории подобия (вторая теорема подобия). Она устанавливает число безразмерных комплексов, которые представляют собой критерии подобия и отвечает на вопрос, как обрабатывать результаты опытов, проводимых на моделях: их надо представлять в виде функциональных зависимостей между критериями подобия, т.е. в виде критериального уравнения. И тогда результаты экспериментов могут быть обобщены на весь класс подобных систем.