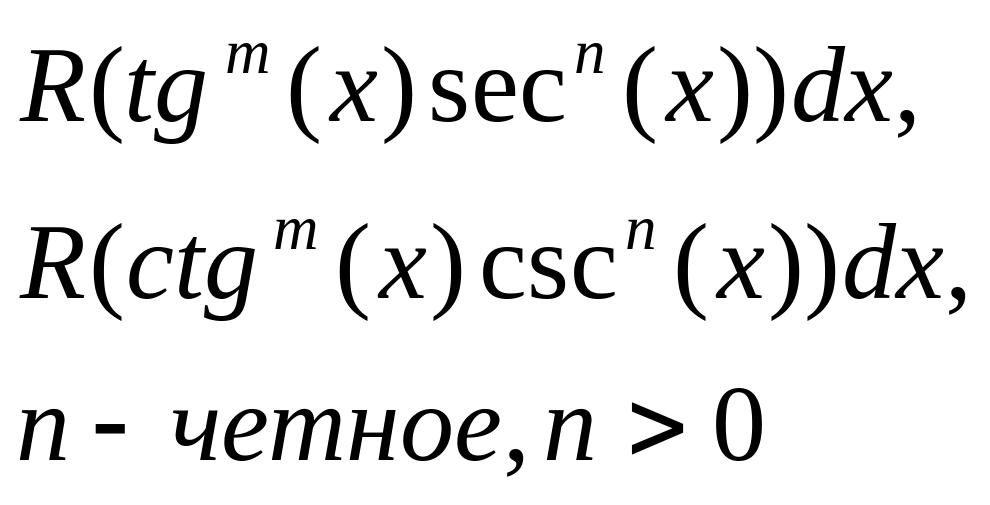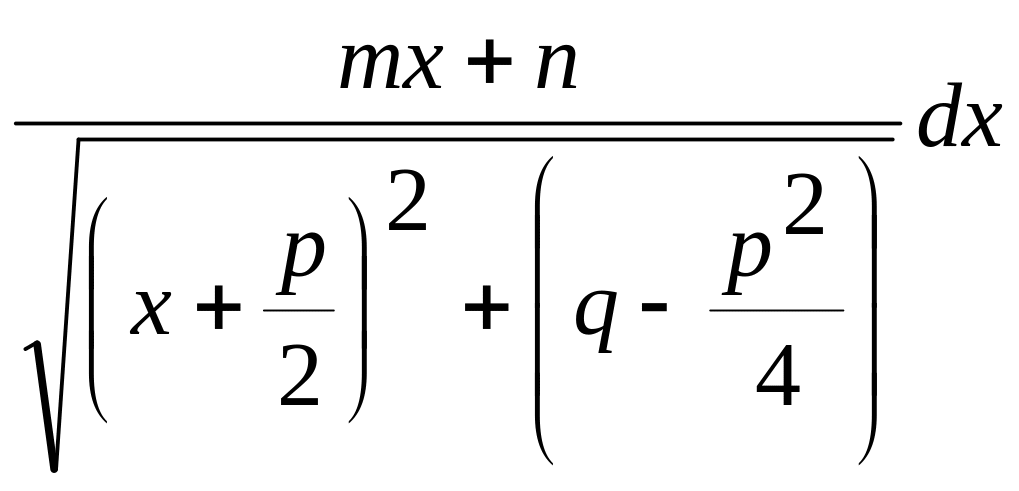7.4. Интегрирование тригонометрических функций

• Метод тождественных преобразований

Пример 6. Найти интегралы функций:

a) .

Решение.

b) .

Решение.

.

• Метод замены переменной

Пример 7. Найти интегралы функций:

а) .

Решение.

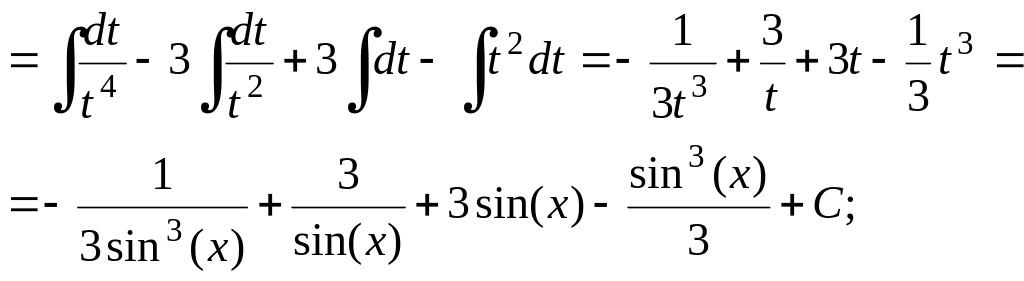
в) .

Решение.

;

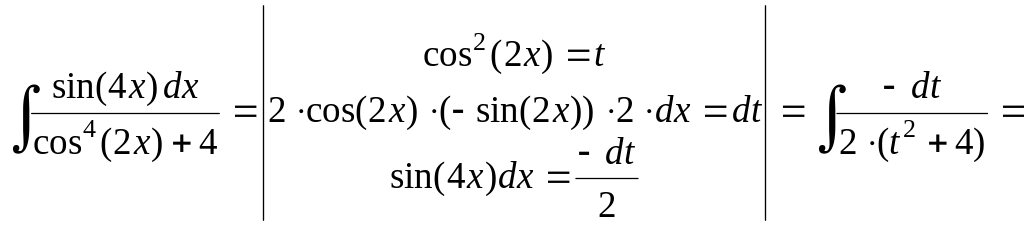
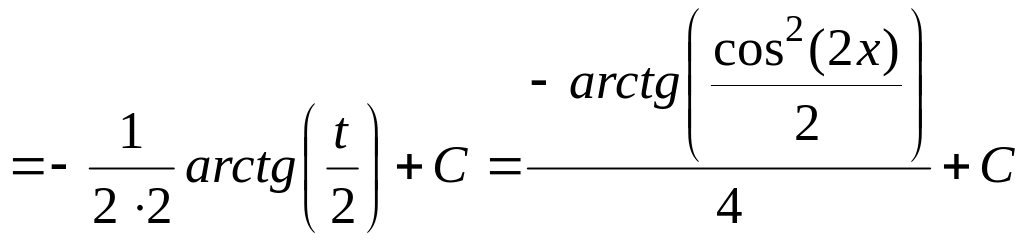с) .

Решение.

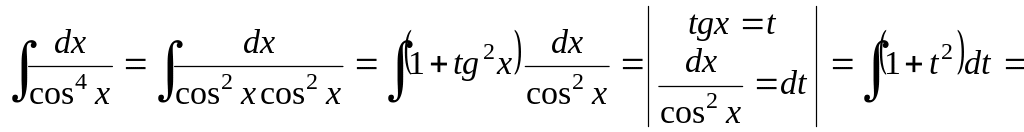
Метод универсальной тригонометрической подстановки

(универсальной замены)

Пример 8. Найти интегралы функций:

а) .

Решение.

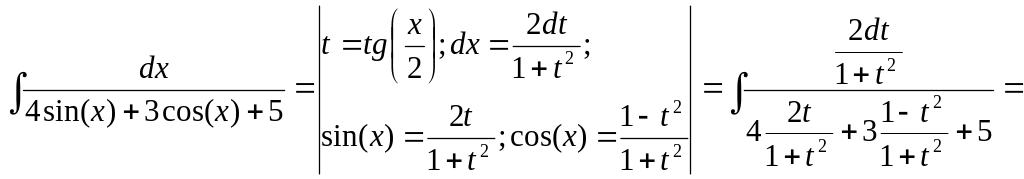
в) .

Решение.

;

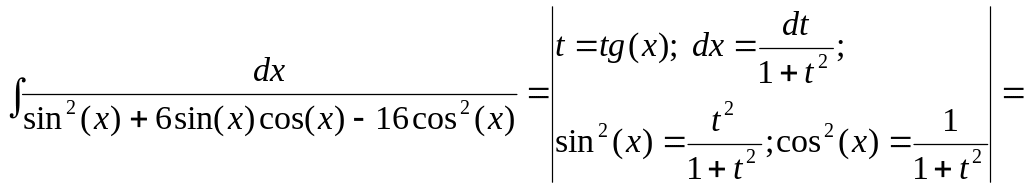
с) .

Решение.

.

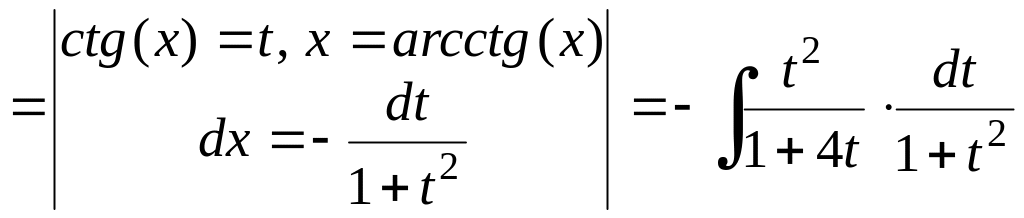Интеграл вычисляется методом неопределенных коэффициентов:

.

.

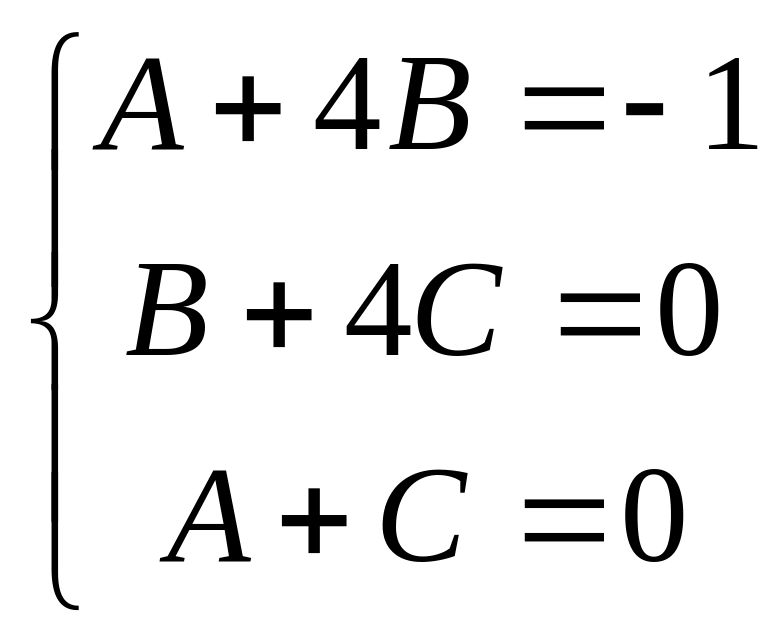
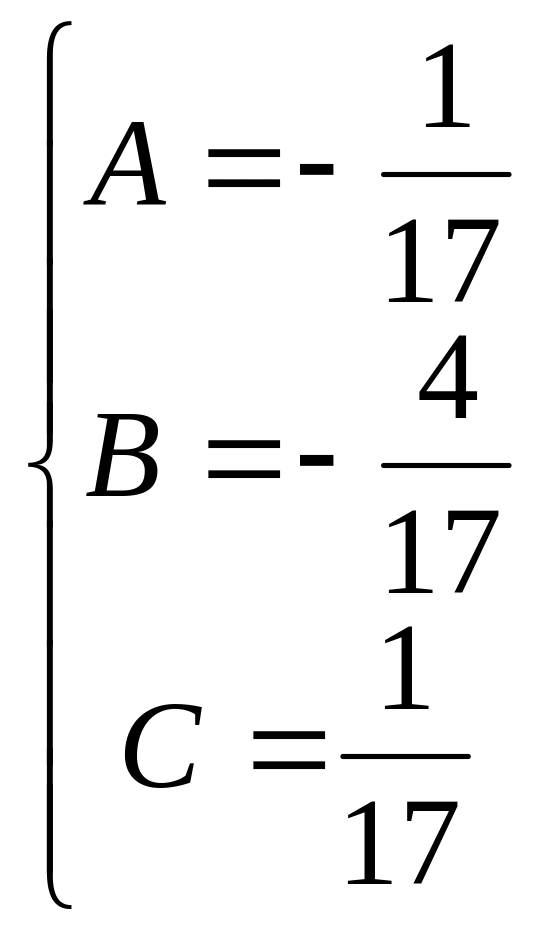Получается:

.

Учитывая выше сказанное, представим основные типы тригонометрических функций в виде таблицы 9.

Таблица 9.

№	подынтегральное выражение	замена
1		Универсальная замена
2
3
4
5
6		, ,
7		Понижается степень по формуле
8

Здесь R – обозначение некоторой рациональной функции от переменных sin(x) и cos(x) . Функции sec(x)=1/cos(x) и csc(x)=cosec(x)=1/sin(x).

7.5. Интегрирование иррациональных функций

Выделяют три основных типа интегралов, содержащих иррациональные функции:

• Первый тип включает в себя интегралы, которые вычисляются методом замены переменной.

Пример 9. Найти интегралы функций:

a) .

Решение.

;

b) .

Решение.

.

с) .

Решение.

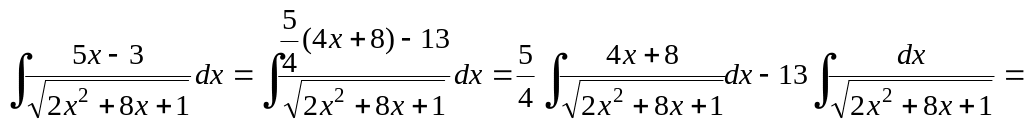
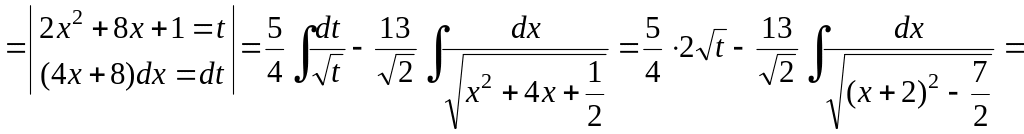
Таким образом, к первому типу можно отнести следующие подынтегральные выражения, представленные в таблице 10.

Таблица 10.

№	подынтегральное выражение	преобразования	замена	dx
1
2
3
4			,
5	, где

• Ко второму типу относят интегралы вида 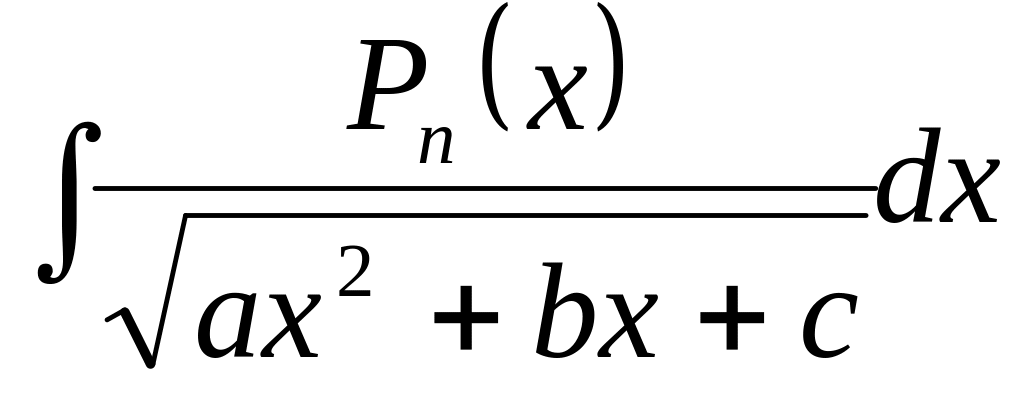, где P_n(x) – многочлен п-ой степени. Интеграл находится методом неопределённых коэффициентов, с помощью тождества:

= ,

где Q_n-1(x) – многочлен степени равной п-1 с неопределёнными коэффициентами, λ – некоторый неопределённый коэффициент.

Пример 10. Найти интегралы функций:

а) .

Решение.

Здесь n = 3, поэтому соответствующее тождество имеет вид:

.

Продифференцируем полученное выражение:

.

Умножим на и сгруппируем коэффициенты при одинаковых степенях х:

=

=

.

Итого =

= ;

b) .

Решение.

Здесь n = 4, поэтому соответствующее тождество имеет вид:

.

Дифференцируем полученное выражение:

_.

Перегруппировываем:

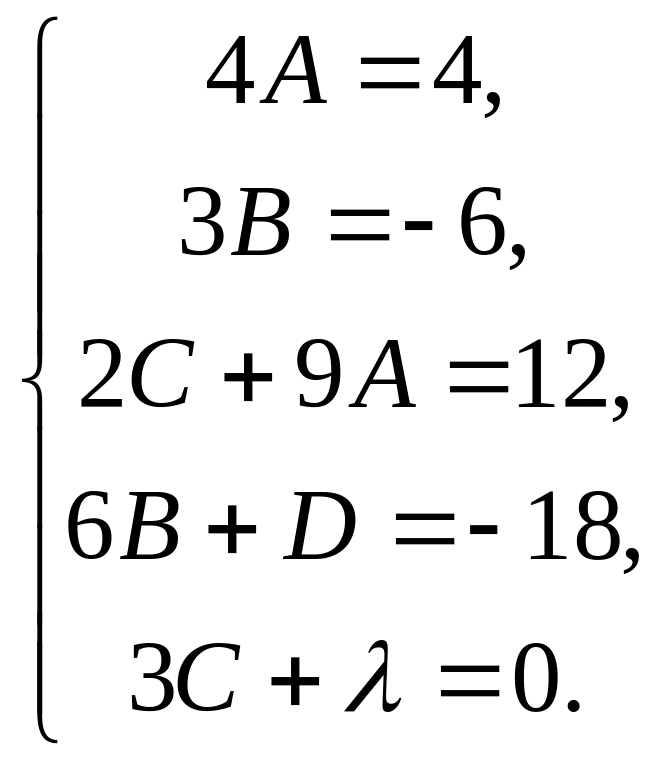
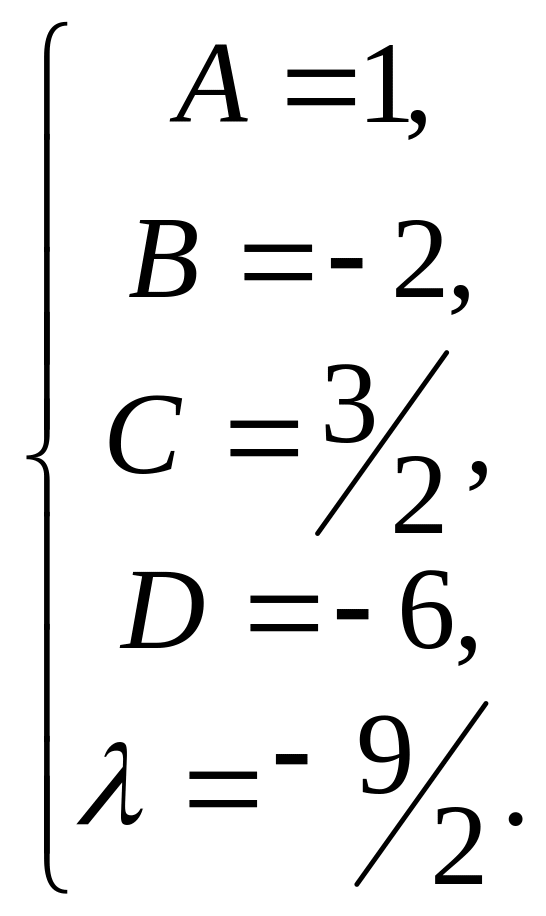
• К третьему типу относят интегралы вида .

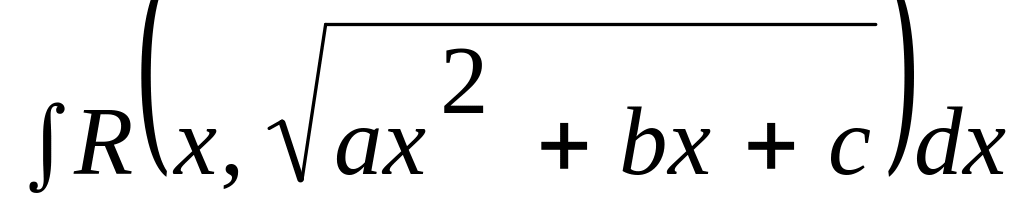Интегрируются с помощью тригонометрической подстановки, которая называется подстановкой Эйлера. При необходимости выделяют под радикалом полный квадрат, т.е. , и вводят обозначение: , .

Пример 11. Найти интегралы функций:

a) .

Решение.

;

b) .

Решение.

;

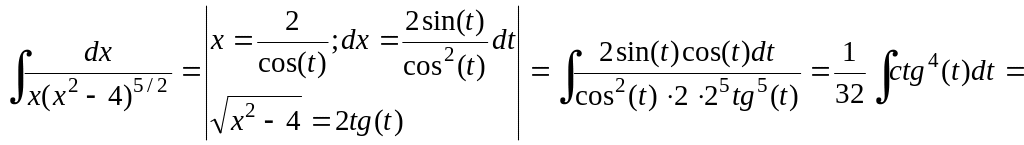
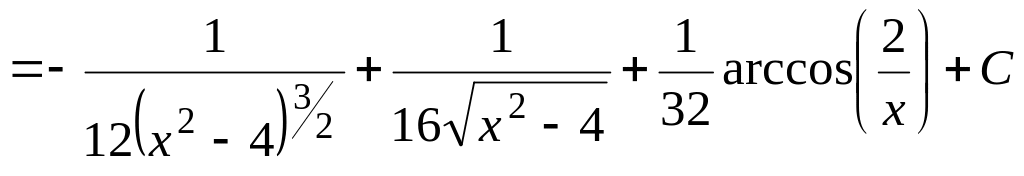с) .

Решение.

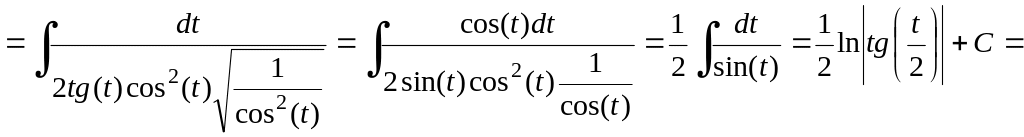
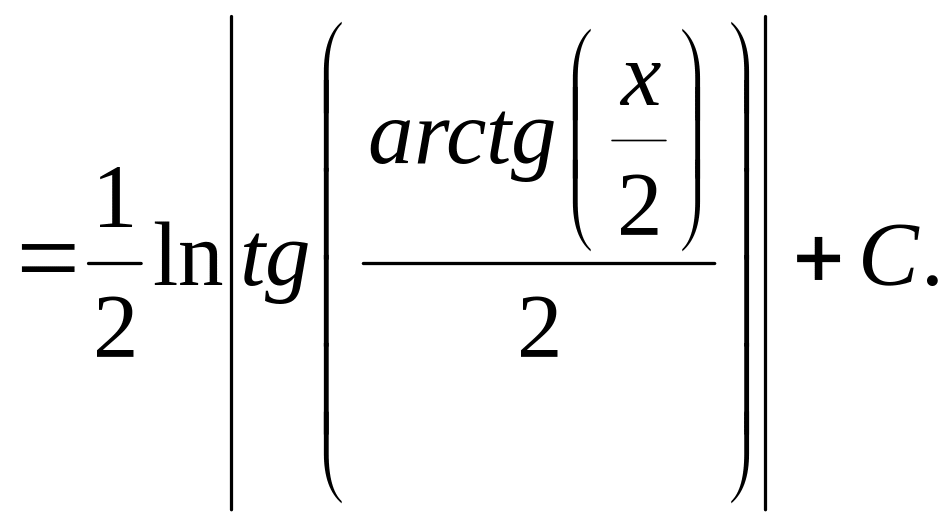
Таким образом, введя новые обозначения имеем следующие подынтегральные выражения, которые будут иметь соответствующие тригонометрические подстановки, представленные в таблице 11.

№	подынтегральное выражение	замена	dt
1		или	или
2		или	или
3		или	или

Таблица 11.