Метод Бернулли

Запишем функцию в виде произведения двух функций . Находим производную . Подставим все в данное уравнение или выражение в квадратных скобках приравняем к нулю. Отсюда , тогда для отыскания получим уравнение .

Сначала найдем из уравнения – ДУ с разделяющимися переменными: , , , придадим с любое значение, пусть , тогда .

Зная , найдем из уравнения : – уравнение с разделяющимися переменными, отсюда .

Найдем искомую функцию : – эта формула дает общее решение линейного уравнения.

Замечание. Формулу запоминать не имеет смысла, необходимо помнить алгоритм решения.

Пример 8. Решить уравнение .

Решение. Положим ; тогда . Имеем:

, . (1)

, тогда .

Значит . Пусть , тогда .

Для нахождения функции вернемся к уравнению (1): , , , .

Зная, и окончательно имеем: .

2.7. Уравнение Бернулли

Уравнение вида , где и , называется уравнением Бернулли. Данное уравнение также решают методами Лагранжа или Бернулли.

Решите самостоятельно ДУ любым из указанных методов.

2.8. Уравнения в полных дифференциалах

Если для дифференциального уравнения выполнено равенство , то оно может быть представлено в виде . Такое уравнение называется ДУ в полных дифференциалах.

Общий интеграл уравнения есть . Функция определяется по формуле 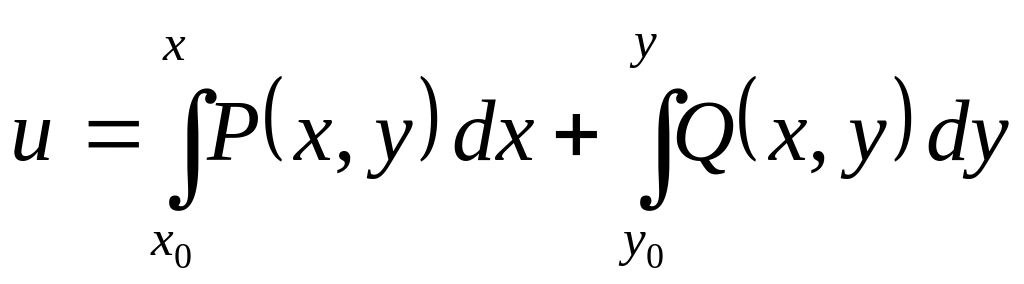, где x₀ и y₀ – подбираются произвольным образом. Если необходимо найти интегрирующий множитель (рекомендуем эту тему разобрать самостоятельно).

Пример 9. Найти общий интеграл уравнения .

Решение. Þ левая часть ДУ есть полный дифференциал некоторой функции . Найдем ее:

.

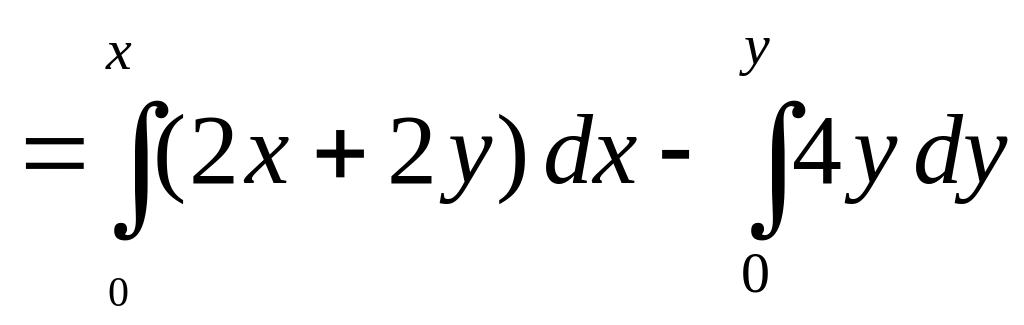
Так как C, получим .

2.9. Дифференциальные уравнения высших порядков. Основные понятия

Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае имеет вид , или в виде, разрешенном относительно старшей производной , если это возможно.

Решением ДУ второго порядка называется всякая функция , которая при подстановке в уравнение обращает его в тождество.

Общим решением ДУ второго порядка называется функция , где и – произвольные постоянные, удовлетворяющая условиям: 1) – является решением ДУ для каждого фиксированного значения и ; 2) каковы бы ни были начальные условия , , существуют единственные значения постоянных и такие, что функция является решением данного уравнения и удовлетворяет начальным условиям.

Всякое решение данного ДУ, получающееся из общего решения при конкретных значениях постоянных и , называется частным решением.

Решения ДУ, записанные в виде , , называются общим и частным интегралом соответственно.

График всякого решения ДУ второго порядка называется интегральной кривой. Общее решение представляет собой множество интегральных кривых; частное решение – одна интегральная кривая этого множества, проходящая через точку и имеющая в ней касательную с заданным угловым коэффициентом .

Как и в случае ДУ первого порядка, задача нахождения решения ДУ, удовлетворяющая заданным начальным условиям, называется задачей Коши.

Теорема (существования и единственности задачи Коши). Если в ДУ функция и ее частные производные и непрерывны в некоторой области D изменения переменных х, у и , то для всякой точки существует единственное решение данного ДУ, удовлетворяющее начальным условиям , .

Аналогичные понятия и определения имеют место для ДУ п-го порядка, которое в общем виде записывается как .

Задача нахождения решения ДУ п-го порядка сложнее, чем первого, поэтому ограничимся рассмотрением отдельных видов ДУ высших порядков.