Московский АВИАЦИОННЫЙ ИНСТИТУТ

Факультет № 3 «Системы управления, информатика и электроэнергетика»

Кафедра № 301

«Системы автоматического и интеллектуального управления»

ЛЕКЦИЯ № 6

по дисциплине «Физические основы получения информации»

Модуляция сигналов

Автор: профессор кафедры № 301

д.т.н., доцент КНЯЗЕВ В.В.

Москва 2017 г.

Лекция № 6. Модуляция сигналов

Цель занятия: Ознакомление студентов с основами модуляции.

Время: 2 часа.

Учебные вопросы:

Вопрос 1. Непрерывная модуляция сигналов 2

Вопрос 2. Импульсная модуляция сигналов 8

Литература:

1. Системы электросвязи: Учебник для вузов/ В.П. Шувалов, Г.П. Катунин, Б.И. Крук и др.; Под ред. В.П. Шувалова. –М.: Радио и связь, 1987. 512 с.

Введение

Чтобы передать информационный сигнал в системе электросвязи, нужно воспользоваться каким-либо переносчиком.

В качестве переносчика естественно использовать те материальные объекты, которые имеют свойство перемещаться в пространстве, например электромагнитное поле в проводах (проводная связь), в открытом пространстве (радиосвязь), световой луч (оптическая связь).

Таким образом, в пункте передачи первичный электрический сигнал s(t) необходимо преобразовать в сигнал v(t), удобный для его передачи по соответствующей среде распространения, но наделенный в то же время признаками первичного сигнала.

В пункте приема выполняется обратное преобразование.

Рис.В.1. Принцип передачи сигналов электросвязи

В отдельных случаях (например, когда средой распространения является пара физических проводов, как в городской телефонной связи) указанное преобразование сигнала может отсутствовать.

Вопрос 1. Непрерывная модуляция сигналов

Обычно в качестве переносчиков используют гармоническое колебание высокой частоты — несущее колебание.

Процесс преобразования первичного сигнала заключается в изменении одного или нескольких параметров несущего колебания по закону изменения первичного сигнала (т. е. в наделении несущего колебания признаками первичного сигнала) и называется модуляцией¹.

Запишем гармоническое колебание, выбранное в качестве несущего, в следующем виде:

v₀(t) = V cos(ωt + φ). (1.1)

Это колебание полностью характеризуется тремя параметрами: амплитудой V, частотой ω и начальной фазой φ.

Модуляцию можно осуществить изменением любого из трех параметров по закону передаваемого сигнала.

1.1. Амплитудная модуляция.

Изменение во времени амплитуды несущего колебания пропорционально первичному сигналу s(t), т. е.

V(t) = V+ k_AM s(t),

где k_AM – коэффициент пропорциональности.

Несущее колебание (1.1) с модулированной по закону первичного сигнала амплитудой описывается выражением:

v(t) = V (t) cos (ωt + φ).

Возьмем в качестве первичного информационного сигнала тоже гармоническое колебание, но с более низкой частотой Ω

s(t) = S cos Ω t.

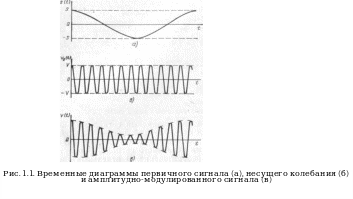Тогда модулированное колебание запишется в виде (для упрощения взято φ = 0)

v(t) = (V + k_AM S cos Ωt)cos ωt.

Вынесем за скобки V и обозначим ΔV = k_AM S и M_AM = ΔV/V:

v(t) = V (1+ M_AM cos Ωt)cos ωt. (1.2)

Параметр M_AM = ΔV/V называется глубиной амплитудной модуляции.

При M_AM = 0 модуляции нет и v(t)= v₀(t), т.е получаем немодулированное несущее колебание.

Амплитуда несущего колебания выбирается не меньше амплитуды первичного сигнала, так что M_AM  1.

Произведем в (1.2) перемножение, используя известное тригонометрическое тождество

и получим амплитудно-модулированное колебание

v (t) = V cos ωt + (М_АМ V/2) cos (ω + Ω) t + (М_АМ V/2) cos (ω – Ω) t (1.3)

Оно состоит из суммы трех гармонических составляющих с частотами ω, ω + Ω и ω – Ω и амплитудами соответственно V, М_АМ V/2 и М_АМ V/2.

Таким образом, спектр амплитудно-модулированного колебания (или AM колебания) состоит из частоты несущего колебания и двух боковых частот, симметричных относительно несущей, с одинаковыми амплитудами.

Спектр первичного сигнала s(t) приведен на рис. 1.2

Рис.1.2. Спектр амплитудно-модулированного гармоническим колебанием гармонического колебания

Если первичный сигнал сложный и его спектр ограничен частотами Ω_min и Ω_max (рис. 1.3, а), то спектр AM колебания также будет ограничен, ширина спектра будет равна Δf = 2 Ω_max. Спектр будет состоять из несущего колебания и двух боковых полос, симметричных относительно несущей (рис. 1.3. б). Верхняя боковая полоса (ВБП) в точности повторит спектр исходного сигнала, смещенный на константу ω, нижняя боковая полоса симметрична нижней относительно ω.

а) б)

Рис.1.3. Спектр амплитудно-модулированного сложным сигналом гармонического колебания

Анализ энергетических соотношений показывает, что основная мощность AM колебания заключена в несущем колебании, которое не содержит полезной информации. Нижняя и верхняя боковые полосы несут одинаковую информацию и имеют более низкую мощность.