9.2 Определение изгибающих моментов колонны от расчетных нагрузок

Определяю максимальный момент колонн при загружении 1+2 без перераспределения моментов. При действии длительных нагрузок:

М₁₂ = (α·g+β·υ) ·l² = –(0,092·32,99 + 0,072·59,4) ·6² = –263,228кН·м;

М₂₃ = –(0,083·32,99 + 0,014·59,4) ·6² = –128,512 кН·м;

При действии полной нагрузки:

М₂₁ = –263,228 – 0,072·43,2·6² = –375,202 кН·м;

М₂₃ = –128,512 – 0,014·43,2·6² = –150,285 кН·м.

Разность абсолютных значений опорных моментов в узле рамы при длительных нагрузках ΔМ₁ = 263,228 – 128,512 = 134,716 кН·м; при полных нагрузках ΔМ₂ = 375,202 – 150,285 = 224,917 кН·м.

Изгибающий момент колонны подвала от длительных нагрузок М = 0,4·ΔМ₁ = = 53,89 кН·м;

От полной нагрузки М = 0,4·ΔМ₂ = 89,97 кН·м.

Изгибающий момент колонны первого этажа от длительных нагрузок М = 0,6·ΔМ₁ = 80,83 кН·м;

От полной нагрузки М = 0,6·ΔМ₂ = 134,95 кН·м.

Вычисляю изгибающие моменты колонны, соответствующие максималь­ным продольным силам; для этой цели использую загружение пролетов по схеме 1.

От длительных нагрузок М = (0,092 – 0,086) · (32,99) ·6² = 7,126 кН·м; изгибающие моменты колонн подвала М = 0.4·7,126 = 2,85 кН·м, первого этажа к М = 0,6·7,126 = 4,28 Н·м.

От полных нагрузок М = (0,092 – 0,086) ·59,4·6² = 12,83 кН·м; изгибающие мо­менты колонн подвала М = 0,4·12,83 = 5,132 кН·м; от первого этажа М = 0,6·12,83 = 7,698 кН·м.

10 Расчет прочности средней колонны

10.1 Характеристика прочности бетона и арматуры.

Класс бетона В20 и класс арматуры А400 (принимают такими же, как и для ригеля).

Комбинация усилий (для колонны подвала) N_мах = 3602,6 кН, в том числе от длительных нагрузок N₁ = 2155,4 кН и соответствующий момент M_max = 5,132 кН·м, в том числе от длительных нагрузок M = 2,85 кН·м

Max M = 89,97 кН·м, в том числе М₁ = 53,89 кН·м.

10.2 Подбор сечений симметричной арматуры.

A_s = A_s^’ выполняют по двум комбинациям усилий и принимают большую площадь сечения. Анализом усилий часто можно установить одну расчетную комбинацию и по ней выполнять подбор сечений арматуры. Здесь проведем расчет по второй комбинации усилий.

Рабочая высота сечения h₀ = h – a = 40 – 4 = 36 см, ширина b = 40

Эксцентриситет силы e₀ = M/N = 89,97/3602,6 = 0,025 м.

Случайный эксцентриситет: e₀ = h/30 = 40/30 = 1,3 см или e₀ = l_col/600 = = 400/600 = 0,67 см, но не менее 1 см.

Поскольку эксцентриситет силы e₀ = 2,05 см больше случайного эксцентриситета e₀ = 1,3 см, его и принимают для расчета статически неопределенной системы.

Находя значение моментов в сечении относительно оси, проходящей через центр тяжести наименее сжатой (растянутой) арматуры. При длительной нагрузке M_1l = M_l + N_l(h/2–a) = 53,89 + 2155,4·0,16=398,75 кН·м, при полной нагрузке М₁ = 89,97 + 3602,6·0,16 = 666,386 кН·м.

Отношение l₀/r = 400/11,56 = 34,6 > 14, где r = 0,289·h = 0,289·41 = 11,85 –радиус ядра сечения.

Вычисляем критическую силу

где D – жесткость железобетонного элемента.

D = k_b·E_b·I+k_s·E_s·I_s = 0,15·27000·213813,76+0,7·200000·819200=1,155·10¹¹

где Е_b, E_s – модуль упругости соответственно бетона и арматуры;

I_, I_s – момент инерции площадей сечения соответственно бетона и всей продольной арматуры относительно центра тяжести поперечного сечения элемента.

K_s = 0,7;

I = r·A = 11,56²·1600 = 213813,76 см⁴

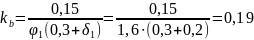
φ1 – коэффициент, учитывающий влияние длительности действия нагрузки.

где Мl1, M1 – моменты относительно центра наиболее растянутого или наименее сжатого стержня арматуры соответственно от действия полной нагрузки и от действия постоянных и длительных нагрузок.

Вычисляем окончательный эксцентриситет:

e = η·(e_n + e₀) = 1· (12,4 + 2,05) = 14,47 см.

e_n = M/N = 447,5/3602,6 = 12,4 м

Вычисляем коэффициент η = 1/(1–N/N_cr) = 1/(1 – 3602,6/2,27·10⁷) = 1,0

Определяют граничную относительную высоту сжатой зоны:

где ω = 0,85 – 0,008·R_b = 0,85 – 0,008·0,9·11,5 = 0,77

Вычисляю:

где δ' = a'/h = 4/36 = 0,111

Определяем площадь арматуры:

Принимаю арматуру: 2Ø36 А400 с Аs=20,36 см4.

μ1= 2·20,36/40·40 = 0,025 – для определения Ncr было принято μ1 = 0,025. Проектирование консоли колонны для опирания ригеля: опорное давление ригеля Q = 257,36 кН.

Бетон класса В20, Rb = 11,5 МПа, γb2=0,90 МПа, арматура класса А400, Rs = 365 МПа. Принимаем длину опорной площади l = 20 см при ширине ригеля lbm = 35 и проверяю условие:

Вылет консоли с учетом зазора 6 см составляет l1 = 26 cм, при этом a = l1 – l/2 = = 26 – 20/2 = 16 cм. Высоту сечения консоли у грани колонны принимают равной h = 0,75·hbm = 0,75·60 = 45 см , при угле наклона сжатой грани γ = 450, высота консоли у свободного края h1 = h – l1 = 45 – 26 = 19 см, при этом h1 = 19 см, что приблизительно h/2 = 45/2 = 22,5 см. Рабочая высота сечения консоли h0 = h – a = = 45 – 3 = 42 см. Поскольку l1 = 26 см < 0,9·h0 = 0,9·42 = 38 см – консоль короткая.

Консоль армируют горизонтальным хомутом Ø6 А240 с Аsw = 2·0,282 = 0,564 см2, шагом s =10 см и отгибами 2Ø18 А240 с As = 5,09 см2.

Проверяю прочность сечения консоли по условию: μw1 = As/b·s = 0,564/40·10 = 0,00141;

α = Es/Eb = 200000/27000 = 7,4;

φw2 = 1+5·α·μw1 = 1 + 5·7,4·0,00141 = 1,052;

sin2θ = h2/(h2+l12) = 452/(452+262) = 0,75;

при этом 0,8·φw2·Rb·b·l·sin2θ = 0,8·1,052·11,5·40·20·0,75· (100) = 580704 Н.

Вычисляю 3,5·Rbt·b·h0 = 3,5·0,9·0,9·40·42 = 476280 Н, следовательно, Q = 257360 H < 476280 H – прочность обеспечена.

Изгибающий момент консоли у грани колонны M = Q·a = 257,36·0,16 = 41,2 кН·м. Площадь сечения продольной арматуры при ζ=0,9 равна:

Принимаю арматуру 2Ø18 А400 с Аs = 5,09 см2.