
Занятие 9
Линейный код задан матрицей
а)
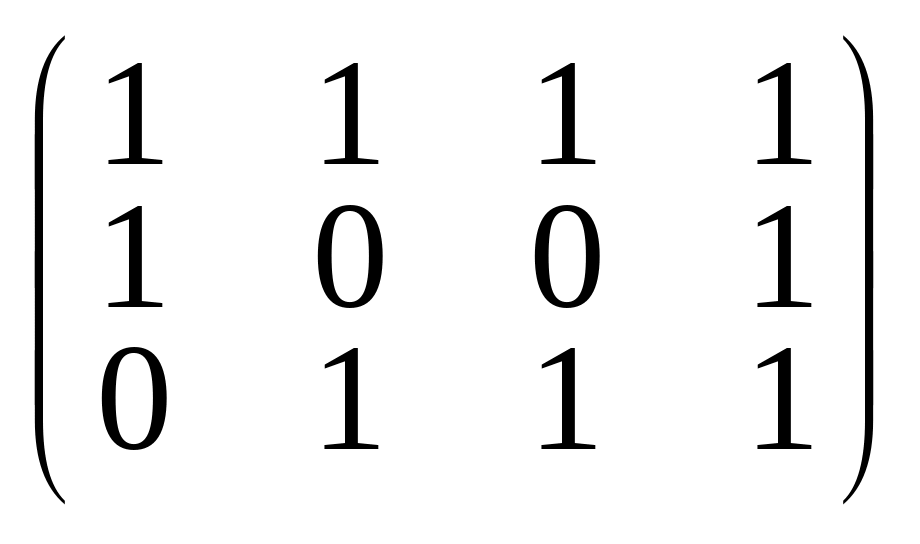 ; б)
; б)
 .
.
Требуется найти:
а) его мощность, кодовое расстояние и характеристическую функцию;
б) мощность, кодовое расстояние и порождающую матрицу двойственного кода.
Сколько контрольных разрядов в коде Хэмминга надо добавить для передачи сообщения, содержащего
а) 22 информационных разряда;
б) 57 информационных разрядов?
С помощью кода Хэмминга требуется передать сообщение
а) (0100111); б) (110100001001).
Получить все кодовые слова кода Хэмминга с числом информационных разрядов, равным
а) 2; б) 3.
Для построенного кода найти:
а) порождающую матрицу;
б) характеристическую функцию двойственного кода.
На выходе канала связи получено кодовое слово кода Хэмминга
а) (1010101001); б) (111011011).
Выяснить, было ли искажение сигнала при передаче по каналу связи? Если да, то что было отправлено на самом деле?
Занятие 10
Решить уравнение
а)
![]() ; б)
; б)
![]() .
.
Команда из 5 человек выступает на соревнованиях, в которых участвуют ещё 20 спортсменов. Сколькими способами могут распределиться места, занятые членами этой команды, если распределение мест внутри команды не важно? А если распределение мест важно?
Сколько можно составить различных расписаний, если расписание одного дня содержит 5 уроков, выбираемых из 11 дисциплин:
а) все дисциплины должны быть различны;
б) дисциплины могут повторяться.
Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить между собой работу? Сколько существует способов, при которых первый почтальон доставит 6 писем?
Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр, если буквы и цифры не должны повторяться? А если буквы и цифры могут повторяться?
Сколько существует способов расположить на шахматной доске две ладьи так, чтобы они били друг друга? Чтобы они не били друг друга? Ответить на эти вопросы для
а) ладей различного цвета; б) ладей одного цвета.
Сколько разных слов можно получить, переставляя буквы слова:
а) «сессия»; б) «коллоквиум»?
В колоде 36 карт. Сколькими способами можно выбрать 8 карт так, чтобы среди них:
а) был ровно один туз; б) был хотя бы один туз?
Занятие 11
Сколько целых неотрицательных натуральных решений имеет уравнение:
а) x + y + z = 20; б) x + y + z = 24?
Сколько натуральных решений имеет это уравнение?
Сколькими способами колоду из 36 карт можно распределить между 4 человеками так, чтобы:
а) всем досталось по 9 карт;
б) всем досталось по 9 карт, причем у каждого был «туз»?
Десять ящиков со стройматериалами нужно доставить на пять этажей. Сколькими способами можно распределить ящики по этажам, если
а) ящики различны; б) ящики не различимы;
в) на каждом этаже оказался хотя бы один ящик (неважно – какой).
На первом этаже в лифт вошли 8 человек. Сколькими способами они могут выйти, если
а) при каждой остановке лифта из него выходит по два человека (кто именно – неважно);
б) при каждой остановке лифта из него выходит по два человека (кто именно – важно);
в) лифт сделал 3 остановки, и на каждой остановке кто-либо вышел (кто именно – неважно);
г) лифт сделал 3 остановки, и на каждой остановке кто-либо вышел (кто именно – важно)?
Шестнадцать человек нужно распределить по 7 вагонам электрички. Сколькими способами это можно сделать так, чтобы
а) в 1-ом и 7-ом вагоне было по 5 человек (кто – неважно);
б) в 1-ом и 7-ом вагоне было по 5 человек (кто именно – важно);
в) все распределились поровну по 4 вагонам (по каким – неважно);
г) все распределились поровну по 4 вагонам (по каким – важно).
В 8 коробок нужно разложить 12 различных мячей. Сколькими способами это можно сделать так, чтобы
а) в первой коробке был всего один мяч (какой – неважно);
б) в первой коробке был всего один мяч (какой – важно);
в) в одной из коробок оказались все мячи (в какой – неважно);
г) в одной из коробок оказались все мячи (в какой – важно)?
В алфавите {a,b,c,d} найдите количество слов длины 6, в которых:
а) буква а встречается на один раз больше, чем b;
б) буква c встречается столько же раз, сколько буквы a и b вместе взятые.
