
Задачи для аудиторных занятий Занятие 1
Граф G задан матрицей смежности:
а)
 ; б)
; б)
 .
.
Нарисовать этот граф. Написать его матрицу инциденций. Есть ли в нем концевые вершины и концевые ребра? Является ли он связным? Ответить на те же вопросы для дополнительного графа.
Нарисовать граф, если степени его вершин:
а) 1,2,2,3,3,5; б) 1,2,2,3,3,4,5.
Является ли он двудольным графом? Есть ли в нем мосты, точки сочленения? Простые циклы? Какой длины?
Сколько ребер в графе
 ,
если в графе G:
,
если в графе G:
а) степени вершин равны 1,1,2,2,3,3?
б) число вершин равно 8, а число ребер – 13?
а) Сколько компонент связности может иметь граф, если в нем 7 вершин и 12 ребер?
б) Сколько вершин может иметь граф, если в нем 10 ребер и 3 компоненты связности?
Граф G задан рисунком:
а) б)


Найти центр, радиус и диаметр графов G и .
Граф задан матрицей инциденций:
а)
 ; б)
; б)
 .
.
Найти расстояние между вершинами 1 и 2. Вычислить удаленность вершины 5. Применить к графу операции:
а) удаления ребра [1,4];
б) удаления вершины 3;
в) отождествления вершин 2 и 4;
г) отождествления вершин 3 и 4;
д) стягивания ребра [3,5].
Какие вершины образуют доли в графе:
а
 )
б)
)
б)
Граф g задан рисунком:
а) б)


Построить эйлеров цикл или эйлерову цепь. Является ли эйлеровым дополнительный граф ? Является ли G гамильтоновым графом?
Занятие 2
Граф g задан матрицей смежности:
а)
 ; б)
; б)
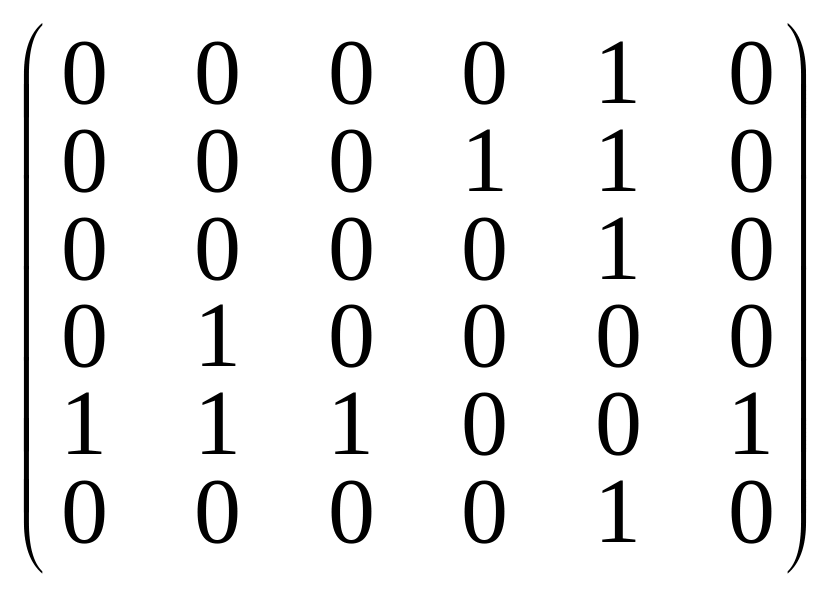 .
.
Является ли граф G деревом? Найти два каких-нибудь остовных дерева графа .
Найти центр, радиус и диаметр дерева:
а
 ) б)
) б)
1 1
Написать его двоичные коды, начиная обход с вершины 1.
Найти центр, радиус и диаметр дерева, заданного двоичным кодом:
а) (0001 0011 1011 0010 1011); б) (0010 0110 1101 0010 11).
Используя «жадный» алгоритм, найти кратчайший гамильтонов цикл в графе с заданной матрицей расстояний (задача коммивояжера):
а)
 ; б)
; б)
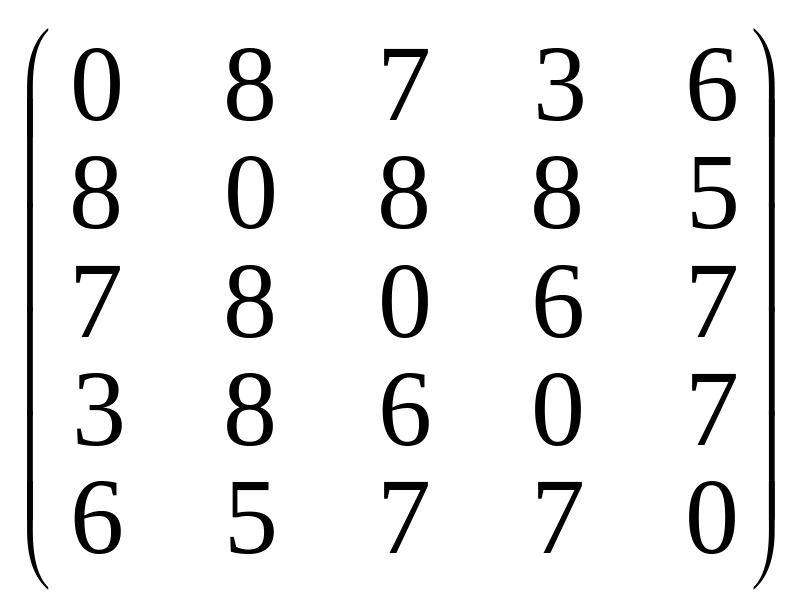 .
.
Применяя алгоритм Дейкстры, найти кратчайшие пути от вершины 1 до остальных вершин графа, заданного матрицей расстояний:
а)
 ; б)
; б)
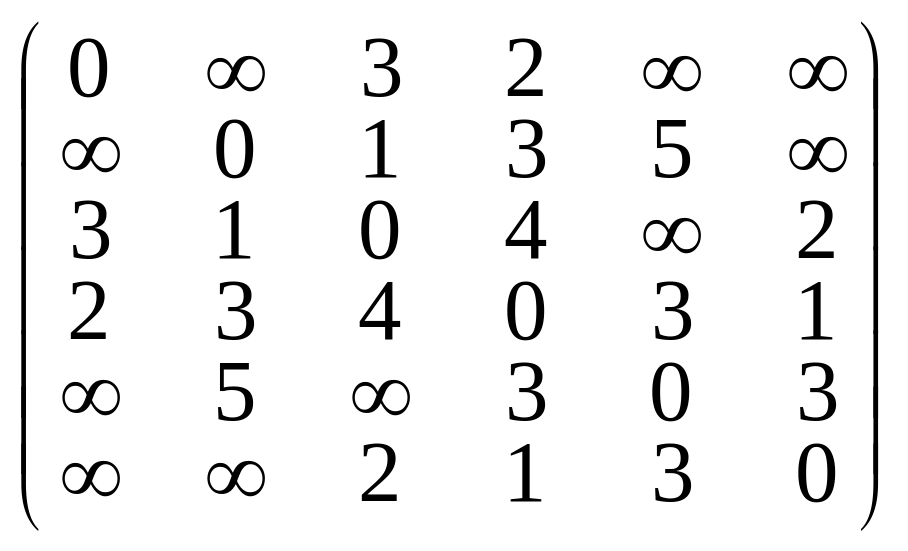 .
.
Используя алгоритм Краскала, найти минимальное остовное дерево графа из примера 5.
Занятие 3
Изоморфны ли графы, изображенные на рисунке:
а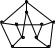
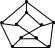 )
)
б
 )
)
в )
)

г)


Г
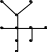 омеоморфны
ли графы:
омеоморфны
ли графы:
а )
)
б
 )
)
Планарны ли графы (в случае планарности найти число граней и проверить формулу Эйлера):
а ) б)
) б)
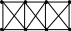
в) г)


Применяя «жадный» алгоритм, найти хроматическое число графа:
а
 ) б)
) б)
Занятие 4
Построить хроматический многочлен графа:
а) б)


Сколько правильных раскрасок можно получить, используя не более 5 цветов?
В рамках чемпионата 5 команд должны провести серию игр так, чтобы каждая команда встретилась с каждой ровно один раз. После нескольких игр выяснилось, что команде А осталось встретиться с командами В, D и Е, команде В – с командами С и Е, команде С – с D, команде D – с Е. Какое минимальное количество дней достаточно, чтобы завершить чемпионат, если команда может проводить не более одной игры в день? Как нужно проводить игры, чтобы завершить чемпионат в кратчайшие сроки?
Три бригады участвуют в выполнении комплекса работ А, B, C, D и Е. Первая бригада выполняет свою часть работ А, B и D, вторая – работ А, C и Е, третья – работ B и C. Каждая бригада выполняет свою часть каждой из указанных работ в течение часа. За какое минимальное количество часов они смогут выполнить весь комплекс работ, если в каждый момент времени бригада может выполнять не более одной работы, и всякая работа может выполняться не более, чем одной бригадой?
Используя алгоритм Демукрона, выполнить топологическую сортировку ориентированного графа, заданного матрицей смежности:
а)
 ; б)
; б)
 .
.
Нарисовать сетевой график и составить список «критических» работ проекта, заданного таблицей:
а)
Работа |
Предшествующие работы |
Длительность работы |
A |
F |
2 |
B |
D |
8 |
C |
B |
2 |
D |
– |
4 |
E |
C, G |
5 |
F |
B |
4 |
G |
B |
3 |
б)
Работа |
Предшествующие работы |
Длительность работы |
A |
E, D |
7 |
B |
C |
3 |
C |
E, D |
6 |
D |
– |
4 |
E |
– |
5 |
F |
A, B |
4 |
G |
C |
5 |
