Результаты решения первой задачи анализа на чувствительность

Наименование Ресурса	Тип ресурса	Максимальное изменение сменного объема запаса, м3	Максимальное изменение сменного дохода от реализации, руб.
Технологические дрова	Дефицитный	83,997-80=+3,997	3422,1-3259,3=162,8
Отходы лесопиления	Недефицитный	39-28=+11	162,8
Объем реализации технологической щепы	Недефицитный	0-20=-20	0
Объем реализации тарной дощечки	Недефицитный	-59,26+0=-59,26	0

5.2. Вторая задача анализа на чувствительность

Введем характеристику ценности дополнительной единицы i-гo ресурса и обозначим ее через Zi. Величина Zi равна отношению максимального приращения оптимального значения у к максимально допустимому приросту объема i-го ресурса.

Определим значения ценностей для каждого из ресурсов. Для ресурсов технологических дров ценность Z₁ = 162,8 / 3,997 = 40,73 руб./м³, отходов лесопиления Z₂ = 162,8/11=14,8 руб./м³, спроса на технологическую щепу Z₃ = 0 / 20 = 0 руб./м³, спроса на тарную дощечку Z₄ = 0 / -59,26=0 руб./м³.

На основе полученных данных можно сделать вывод, что для получения наибольшей отдачи от вложения дополнительных средств на развитие производства необходимо их вкладывать в развитие производства технологических дров.

5.3. Третья задача анализа на чувствительность

Запишем целевую функцию в виде у=с_щх_щ+с_дх_д, где с_щ и с_д - стоимость 1 м³ технологической щепы и тарной дощечки соответственно. На рис. 7 отражены направления вращений линии дохода (1) при изменении коэффициентов функции цели. Из рис. 7 ясно, что точка D будет являться оптимальной до тех пор, пока наклон линии функции цели (1) не выйдет за пределы наклонов линий ограничений (2) и (3). Если угол наклона линии (1) равен углу наклона линии (2) - совпадение этих линий, - то получим две альтернативные оптимальные точки С и D или любые другие точки, принадлежащие линии (2) в промежутке между точками С и D. Соответственно, при совпадении линии (1) и (3) – точки С и Е или точки между ними. Как только наклон линии (1) выйдет за пределы наклона линий ограничений (2) и (3), оптимальное решение будет другим – точка Как только наклон линии (1) выйдет за пределы наклона линий ограничений (2) и (3), оптимальное решение будет другим – точка D в первом случае или точка Е во втором.

Для нахождения интервалов изменения цен (коэффициентов функции цели), при котором точка D остается оптимальной, оставим значение с_д = 80 неизменным. Значение с_щ можно увеличивать до тех пор, пока линия у не совпадет с линией (3), или уменьшать до совпадения у с линией (2), то есть углы линий (3) и (2), определяют допустимые углы изменения наклона линии у. Тангенс угла наклона линии у, проходящей через точку D с известным коэффициентом с_д = 80, определяется как

(см. рис.7), а для линий ограничений (2) и (3), исходя из их выражений, соответственно как 1,35/2,5 и 0,45/1,5.

Тогда минимальное значение с_щ определяется из равенства

(равенство углов определяет равенство их тангенсов). На основе изложенного

с_{щ min} = 43,2 руб./м³. Аналогично определяется максимальное значение с_щ

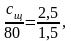с_{щ max} = 133,33 руб./м³.

Интервал изменения с_щ, в котором точка D по-прежнему будет являться оптимальной 43,2 ≤ с_щ ≤ 133,33.

Расчет пределов изменения цен на тарную дощечку осуществляется по аналогичной методике.

Тогда минимальное значение с_д определяется из равенства

(равенство углов определяет равенство их тангенсов). На основе изложенного с_{д min}=33 руб./м³. Аналогично определяется максимальное значение с_д.

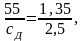с_{д max} = 101,85 руб./м³.

Интервал изменения с_д, в котором точка D по-прежнему будет являться оптимальной

33 ≤ с_д ≤ 101.85.

На примере полученного диапазона цен для технологической щепы можно сделать заключение о том, что в пределах изменения цен от 43.2 до 133.33 рублей за 1 м³ необходимо сохранить прежние объёмы выпуска технологической щепы (х_щ = 59.26 м³) и тарной дощечки (х_д = 0 м³) с целью извлечения максимального дохода, а за пределами представленного диапазона целесообразно изменение объёмов производства х_щ, х_д, что повлечёт трансформацию каких-либо ресурсов из дефицитных в недефицитные и наоборот. Какие необходимы изменения объёмов и какие ресурсы трансформируются, определяется конкретной ситуацией.

Ситуация первая: руководитель предприятия заключает контракт о поставке технологической щепы с представителем потребителя. В процессе торга о цене на щепу может фигурировать любая цифра в пределах от 43.2 до 133.33 руб. за кубометр, а также возможно позволить снижение цены от уровня средней рыночной в пределах выше представленного диапазона за счёт каких-либо встречных обязательств партнёра. Например, поставка дефицитной продукции с его стороны, увеличение объёма потребления щепы и прочее.

Ситуация вторая: по каким-либо причинам произошло снижение сменного объема технологических дров. Поскольку этот ресурс дефицитен, то при сложившихся коэффициентах расхода сырья и структуре технологического процесса снижается объем производства технологической щепы, и увеличивается объем производства тарной дощечки. Для того, чтобы не испытывать затруднений по обязательствам поставок этой продукции – санкции за недопоставки и пр., - снижаем цену на щепу до уровня 43,2 руб. за кубометр и ниже и перестраиваем производство под уровень выпуска в точке С (х_щ=55,56, х_д =2). Этим мы избежим штрафных санкций за счет снижения цены на щепу (если сумеем договорится с партнером) и переведем в разряд недефицитных ресурс отходов лесопиления. Но, возможно, выгоднее окажется заплатить штраф, чем снижать цену и перебрасывать ресурсы, рабочих, сырье – на увеличение производства тарной дощечки. Поэтому в каждом конкретном случае необходимы дополнительные технико-экономические обоснования.