5.2. Проектирование делителей частоты
Под делителем частоты понимается устройство, осуществляющее изменение частоты сигнала на выходе по отношению к входному сигналу в n раз. Параметр n, определяемый отношение частоты сигнала на входе и выходе устройства, называется коэффициентом деления. При анализе и синтезе ДУ все величины отождествляются с множеством целых чисел, поэтому n также принимает целочисленные значения.
Собранный на ДЭ делитель частоты осуществляет преобразование последовательности импульсов, поступающих на его вход, в некоторую последовательность импульсов, получаемых на выходе. На каждые n-импульсов на входе схемы формируется один импульс на её выходе. Длительность формируемых на выходе схемы импульсов может существенно отличаться от длительности импульсов, поступающих на вход.
В качестве делителей частоты можно использовать асинхронные и синхронные счётчики, с равным, требуемому коэффициенту деления, числом устойчивых состояний. При построении делителей частоты не имеет принципиального значения последовательность переключения триггеров счётной схемы, определяющих её промежуточные устойчивые состояния. Важным является только последовательное прохождение схемой n-состояний при поступлении на её вход такого же количества импульсов. Следовательно, используемая в качестве делителя частоты счётная схема может осуществлять счёт в любом коде.
При использовании асинхронных счётчиков необходимо предусмотреть сброс схемы в первоначальное состояние после отсчёта требуемого числа импульсов входного сигнала. Выделение используемой для сброса схемы кодовой комбинации осуществляется с помощью настроенной на данную комбинацию схемы совпадения с последующим инвертированием формируемого сигнала (рис. 5.8, а).
В качестве выхода делителя частоты используют выход одного из входящих в состав схемы триггеров. Выбор триггера осуществляется из условия формирования на его выходе одного импульса на каждые n-импульсов, поступающих на вход делителя частоты (рис. 5.8, б). В качестве выходного сигнала делителя частоты нельзя использовать сигнал, снимаемый с триггера, который за время поступления на вход схемы n-импульсов устанавливается в единичное состояние более одного раза.
Рис. 5.8. Схема делителя частоты на 6 (а) и временная диаграмма его работы (б)
Для построения делителей частоты можно использовать различные типы триггеров. На рис. 5.9 показано использование в качестве делителя частоты асинхронной счётной схемы с М=11, реализованной на JK-триггерах. Благодаря наличию на логических входах J и K уровня логической единицы все триггеры работают в счётном режиме, изменяя своё состояние на противоположное по каждому импульсу, поступающему на вход "С". После поступления на вход ТИ десятого импульса четвёртый и второй триггеры схемы устанавливаются в единичное состояние и на выходе "А" элемента "И–НЕ" формируется используемый для сброса схемы уровень логического нуля. Выходной сигнал делителя частоты снимается с выхода триггера Q4, на котором на каждые 10 импульсов на входе ТИ формируется один импульс (рис. 5.9).
В качестве делителей частоты могут использоваться и синхронные счётные схемы, проектируемые на основании методики, рассмотренной в пункте 5.1.2.
Путём каскадного соединения нескольких схем можно получить делители частоты с различным коэффициентом деления. Например, подавая сигнал с выхода делителя частоты (рис. 5.8, а) на вход ТИ схемы, представленной на рис. 5.9, а, можно получить делитель с коэффициентом деления n = 60.
В большинстве случаев делители частоты с любым коэффициентом деления могут быть составлены без использования дополнительных логических элементов, т. е. очень экономично. Достоинством таких делителей является простота их схемной реализации. Однако логическое проектирование таких схем требует различных подходов, большого опыта и не может быть формализовано в виде общей, применимой во всех случаях, методики. Некоторые схемы делителей частоты, построенные без использования дополнительных элементов, представлены на рис. 5.10–5.15. Помимо схем на каждом рисунке также представлены поясняющие работу рассматриваемых делителей временные диаграммы [3].
Рис. 5.9. Схема делителя частоты на 10, реализованного с использованием JK-триггеров (а) и временная диаграмма его работы (б)
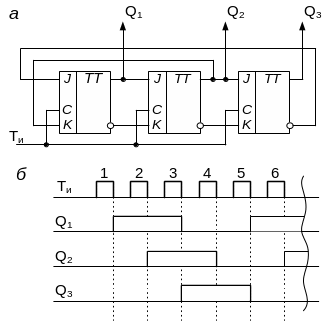
Рис. 5.10. Схема делителя частоты на 5 без использования дополнительных логических элементов (а) и временная диаграмма его работы (б)
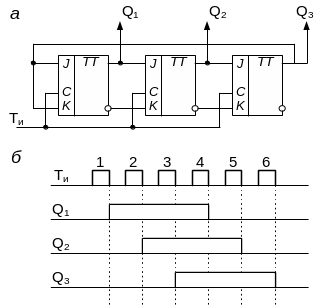
Рис. 5.11. Схема делителя частоты на 6 без использования дополнительных логических элементов (а) и временная диаграмма его работы (б)
Рис. 5.12. Схема делителя частоты на 7 без использования дополнительных логических элементов (а) и временная диаграмма его работы (б)
Рис. 5.13. Схема делителя частоты на 9 без использования дополнительных логических элементов (а) и временная диаграмма его работы (б)
Рис. 5.14. Схема делителя частоты на 10 без использования дополнительных логических элементов (а) и временная диаграмма его работы (б)