5.1.2. Логическое проектирование синхронных счётных схем

Проектирование синхронных счётных схем основывается на использовании более формализованных математических методов. Синтезируемая схема представляется в виде логической структуры, состоящей из n-триггеров, используемых в качестве элементов памяти, и некоторой комбинационной схемы (рис. 5.3, а). Сигналы с выходов триггеров поступают на входы комбинационной схемы. Сигналы с выходов комбинационной схемы поступают на информационные входы триггеров. Количество триггеров, требующихся для реализации счётной схемы с модулем М, определяется по формуле .

таким образом, комбинационная схема производит преобразование поступающей на ее входы информации, с тем, чтобы с приходом очередного считываемого импульса осуществить требуемый переход счетчика из предыдущего состояния в последующее. Функции возбуждения Е₁, Е₂, каждого i-го триггера определены для одного и того же момента времени, как и их аргументы, представляющие собой выходные сигналы триггеров счетной схемы:

;

.

Следовательно, данные функции являются переключательными. Структура комбинационной схемы полностью определяется формируемыми ею функциями возбу­ждения триггеров. Поэтому при выбранном ти­пе используемых триггеров задача логическо­го проектирования счетной схемы заключается в составлении функций возбу­ждения каждого триггера и минимизации этих функций в заданном базисе.

При оп­ределении функций возбуждения каждого триггера схемы используют составленные для данного типа триггера матрицы переходов (рис. 5.3, б).

Каждая строка матрицы соответствует одному из совершаемых каждым триггером возможных четырёх переходов: , , и . Необходимые для выполнения данного перехода значения функций возбуждения опре­деляют на основании алгоритма функционирования рассматриваемого типа триггера. Например, для выполнения D-триггером переходов и на вход триггера необходимо подать "0", а для переходов и , D должно быть равно "1" (см. рис. 5.3).

Если совершаемый переход полностью определяется одной функцией возбуждения триггера, то в качестве значения другой записывается символ "X", указывающий, что данная функция может принимать любое значение.

Рис. 5.3. Представление счётной схемы в виде логической структуры (а) и матрицы переходов для различных типов триггеров (б)

При записи матрицы для DV-триггера для некоторых переходов вместо чис­ленных значений функций использованы неопределенные коэффициенты: , , , , каждый из которых может принимать значение "0" или "1". Использование неопределенных коэффициентов обусловлено со­вершением переходов и при трех возможных набо­рах функций возбуждения D и V. Например, переход для D=0 может происходить при любом значении сигнала на входе V, а для D=1 – только при подаче на вход V логического нуля. Следовательно, если соответствующее данному переходу значение функции D обозначить через , то для определения V необходимо записать: .

Методику логического проектирования синхронных счетных схем рассмотрим на примере синтеза на JK-триггерах счётчика с М=10, называемого двоично-десятичным счетчиком. Данный счётчик последовательно переходит из одного состояния в другое под действием, поступающих на его вход тактовых импульсов. Каждому состоянию счётчика соответствует своё двоичное число, считываемое с выходов схемы – и определяемое номером состояния счётчика.

При построении рассматриваемой счётной схемы необходимо использовать четыре триггера (Т₁, Т₂, Т₃, Т₄). С целью определения функций возбуждения каждого триггера схемы составляется кодированная таблица переходов (табл. 5.1), в ко­торой любому состоянию схемы ставится в соответствие определенное двоичное число. В левой части таблицы для моментов времени t (t =0, 1, ..., М) последовательно указываются все устойчивые состояния счет­ной схемы, а также состояния, в которые схема переходит в моменты времени t+1 (t = 1, 2,…,М, 0), т. е. после приема каждого следующего импульса. В правой части таблицы указываются значения функций возбуждения каждого триггера, необходимые для осуществления его перехода из состояния, определенного для момента времени t в состояние, определенное для момента времени t+1.

Таблица 5.1

Таблица переходов и требуемых для их реализации значений функций возбуждения счётчика

№ SI	Значения выходов до и после поступления импульса								Значения функций возбуждения триггеров
	t				t+1				T4		T3		T2		T1
	Q4	Q3	Q2	Q1	Q4	Q3	Q2	Q1	J4	K4	J3	K3	J2	K2	J1	K1
0	0	0	0	0	0	0	0	1	0	X	0	X	0	X	1	X
1	0	0	0	1	0	0	1	0	0	X	0	X	1	X	X	1
2	0	0	1	0	0	0	1	1	0	X	0	X	X	0	1	X
3	0	0	1	1	0	1	0	0	0	X	1	X	X	1	X	1
4	0	1	0	0	0	1	0	1	0	X	X	0	0	X	1	X
5	0	1	0	1	0	1	1	0	0	X	X	0	1	X	X	1
6	0	1	1	0	0	1	1	1	0	X	X	0	X	0	1	X
7	0	1	1	1	1	0	0	0	1	X	X	1	X	1	X	1
8	1	0	0	0	1	0	0	1	X	0	0	X	0	X	1	X
9	1	0	0	1	0	0	0	0	X	1	0	X	0	X	X	1

В качестве примера рассмотрим первую строчку табл. 5.1. Счетчик из состояния S₀ (рис. 5.4), соответствующего следующему состоянию триггеров: Q₄ = 0, Q₃ = 0, Q₂ = 0, Q₁ = 0, после поступления очередного считываемого импульса должен перейти в состояние S₁, определяемое как: Q₄ = 0, Q₃ = 0, Q₂ = 0, Q₁ = 1. Следовательно, для триггеров Т₄, Т₃, Т₂ необходимо реализо­вать переход 00, а для триггера Т₁ – переход 01. В соответствии с матрицей переходов JK-триггера (см. рис. 5.4) выбираем значения функций возбуж­дения, необходимые для осуществления данного перехода: J₁ = 0, К₄ = Х, J₃ = 0, К₃ = Х, J₂ = 0, К₂ = Х, J₁ = 1, К₁ = Х.

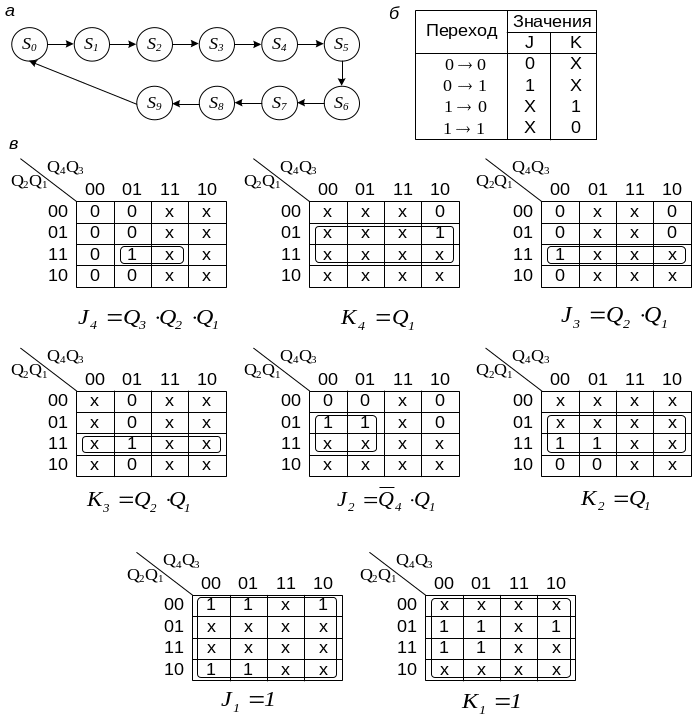
Рис. 5.4. Последовательность изменения состояний счётной схемы и минимизация функций возбуждения триггеров

Из состояния S₁ (см. вторую строку табл. 5.1), определяемого положением триггеров: Q₄ = 0, Q₃ = 0, Q₂ = 0, Q₁ = 1, счётная схема должна перейти в состояние S₂, соответствующее: Q₄ = 0, Q₃ = 0, Q₂ = 1, Q₁ = 0. Поэтому для триггеров Т₄, Т₃ необходимо реализо­вать переход 00, для триггера Т₂ – переход 01, для триггера Т₁ – переход 10. В соответствии с матрицей переходов JK-триггера (см. рис. 5.4) находим: J₄ = 0, К₄ = Х, J₃ = 0, К₃ = Х, J₂ = 1, К₂ = Х, J₁ = Х, К₁ = 1. Остальные строки таблицы запол­няются аналогично.

Для определения функций возбуждения триггеров воспользуемся методом карт Карно. Каждую из восьми функций записываем в карту и производим минимизацию данной функции (см. рис. 5.4).

Структура счетчика, полученная на основе минимизированных функ­ций возбуждения каждого триггера схемы, представлена на рис. 5.5, а. Временная диаграмма работы синтезированной схемы, характеризующая изменение сигналов на выходах триггеров при поступлении синхроимпульсов, приведена на рис. 5.5, б.

Рис. 5.5. Схема синтезированного двоично-десятичного счётчика (а) и временная диаграмма его работы (б)

При использовании других типов триггеров синтез синхронных счётных схем осуществляется аналогично рассмотренному выше примеру, с использованием построенной для данного типа триггера матрицы переходов (см. рис. 5.3) Пример логического проектирования счётной схемы с М=5 на D-триггерах приведён на рис. 5.6. Синтезируемая схема осуществляет счёт в двоичном коде от нуля до четырёх. Под действием поступающих на вход схемы управляющих сигналов Т_И счётчик последовательно переходит из одного состояния в другое, формируя на выходах триггеров двоичный эквивалент номера соответствующего состояния S_i (рис. 5.6).

Полученная по результатам синтеза схемная реализация счётчика и временная диаграмма его работы при поступлении синхроимпульсов приведены на рис. 5.6.

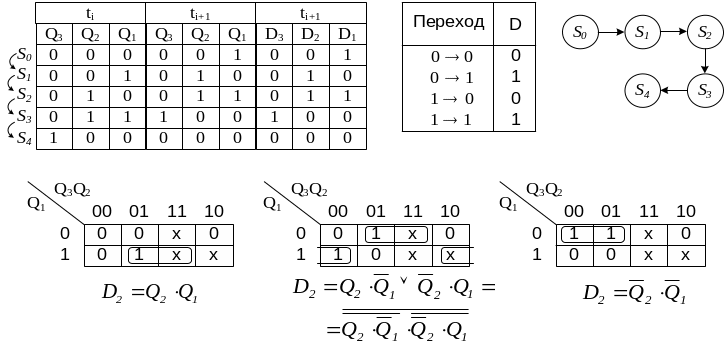
Рис. 5.6. Пример синтеза на D-триггерах синхронного двоичного счётчика с М=4

При синтезе счетной схемы на DV-триггерах в ряде полей карт Карно вместо символа "X" будут вписаны неопределенные коэффициенты. В этом случае карты для D и V функций возбуждения каждого триггера необходимо рассматривать совместно, выбирая накрытия с учетом взаимосвязи полей карт, включающих неопределенные коэффициенты. Например, если для одной из карт коэффициент a_i принят, равным "1", то в поле другой карты произведение, содержащее , независимо от зна­чения , запишется как "0".

Рис. 5.7. Схема счётчика (а) и временная диаграмма его работы (б)