4.2.2. Синхронные триггеры

Все триггеры можно подразделить на асинхронные и синхронные. Изменение состояния асинхронного триггера происходит при изменении сигналов на его управляющих входах. Переключение триггера в противоположное состояние происходит с запаздыванием, определяемым только временем распространения сигнала внутри схемы. Синхронные триггеры, кроме информационных входов, снабжены дополнительным входом "С". Поступающие на этот вход синхронизирующие импульсы задают моменты переключения триггера из одного состояния в другое, определяемое в зависимости от комбинации сигналов на управляющих входах. Поэтому прием новой информации в такой триггер синхронизируется с моментом поступления сигнала на вход "С".

В зависимости от структуры СУ, определяющей логические функции, связывающие входные и выходные переменные, можно получить различные типы триггеров, существенно отличающиеся друг от друга алгоритмом функционирования. Основными из нашедших наиболее широкое применение типов триггеров являются RS, D, DV, JK, T. Условные обозначения перечисленных типов триггеров представлены на рис. 4.4.

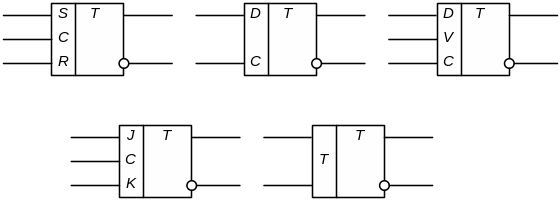
Рис. 4.4. Основные типы триггеров

Синхронный RS-триггер, как и асинхронный, рассмотренный ранее, имеет два логических входа: вход " S " – установка в "1" и вход " R " – установка в "0". При отсутствии сигнала логической единицы на обоих входах схемы (S=0, R=0) состояние триггера не изменяется. Комбинация сигналов S=1; R=1 для данного типа триггера является запрещенной. Кроме логических входов, синхронный RS-триггер снабжен специаль­ным входом "С", используемым для подачи синхронизирующих импульсов. Наличие данного входа не изменя­ет логический алгоритм функционирования триггера. Однако переход триггера из одного состояния в другое возможен только при подаче синхронизирующего импульса на вход "С".

В ряде случаев при проектировании различных устройств необходимо допускать появление на входе RS-триггера запрещенной комбинации S=1; R=1. Поэтому наряду с типовым RS-триггером используются его различные модификации, обозначаемые как E-, R-, S-триггеры. В за­висимости от состояния, в которое устанавливается триггер при дейст­вии на его входы запрещенной комбинации, RS-триггер подразделяется на следующие типы: Е-триггер – со­стояние не изменяется, R-триггер – сбрасывается в ноль и S-триггер – устанавливается в единицу.

D-триггер (рис. 4.4) имеет один логический вход D, состояние которого с каж­дым синхронизирующим импульсом передается на выход. Чтобы уста­новить триггер в "1", необходимо при наличии единичного сигнала на входе D подать синхроимпульс. Поступление синхроимпульса при нуле­вом сигнале на входе D вызывает установку триггера в нуль. Данный тип триггера используется для задержки сигнала на один такт.

DV-триггер работает аналогично D-триггеру и отличается от него на­личием дополнительного входа V, служащего для запрета приема син­хронизирующего импульса. Следовательно, при наличии на входе V сиг­нала логической единицы, DV-триггер функционирует как D-триггер. При подаче на вход V логического нуля триггер перестает реагировать на поступление синхроимпульсов и изменение сигнала на входе D.

JK-триггер имеет два логических входа J и К (см. рис. 4.4). Для уста­новки триггера в "1" необходимо подать синхроимпульс при наличии на входе J сигнала логической единицы, а на входе К – логического нуля. Поступление синхроимпульса при J = 0, К = 1 приводит к установке триг­гера в нулевое состояние. В случае наличия сигнала логической единицы на обоих входах триггера J = 1, К = 1 он изменяет свое состояние по каждому синхроимпульсу. Поступление синхроимпульсов при нулевом уровне сигналов на логических управляющих входах (J = 0, К = 0) не вызывает изменения состояния триггера.

Т-триггер имеет один информационный вход и носит название счетного триггера, который работает в счётном режиме, изменя­я свое состояние на противоположное при поступлении на вход Т каждого синхроимпульса.

Для синтеза синхронных триггерных схем используют методику, аналогичную применяемой при синтезе асинхронных триггеров. Пример логического проектирования D-триггера представлен на рис. 4.5. Синтез данного синхронного триггера также начинается с составления структурной схемы синтезируемого триггера и таблицы (рис. 4.5, а), отражающей значение каждой из искомых функций f₁, f₂ при любом возможном наборе аргументов. В качестве аргументов в данном случае используются переменные, определяющие состояние синхронизирующего "С" и логического "D" входов триггера. Нахождение функций возбуждения ЗЯ также необходимо производить с учётом значения выхода Q, характеризующего состояние триггера.

После записи значений функций f₁, f₂ требуемых алгоритмом функционирования триггера на каждом наборе аргументов, осуществляют минимизацию данных функций. Минимизация функций f₁, f₂ выполнена с ис­пользованием карт Карно (рис. 4.5, б). Полученная в результате проведённого синтеза логическая структура тригге­ра представлена на рис. 4.5, в, а его условное графическое обозначение – на принципиальных схемах (рис. 4.5, г).

Рис. 4.5. Синтез D-триггера: таблица задания функций f₁, f₂ (а); минимизация функций методом карт Карно (б); схема синтезированного триггера (в); условное обозначение триггера (г)