3.1. Задачи анализа и логического проектирования комбинационных дискретных устройств

Комбинационным ДУ называется устройство, у которого функция выхода полностью определяется значениями переменных на его входах в данный момент времени. Для построения таких устройств не требуется применения элементов памяти, поэтому функции АЛ могут быть непосредственно использованы при анализе и синтезе комбинационных ДУ.

При реализации нескольких функций АЛ комбинационные устройства имеют несколько выходов, на каждом из которых формируется своя функция. В процессе формирования выходов в различных цепях могут использоваться общие элементы, это позволяет уменьшать их количество в структуре реализуемого ДУ.

Целью анализа схемы комбинационных ДУ является определение алгоритма работы сложных устройств или проверка работоспособности устройства посредством оценки правильности его функционирования в соответствии с требуемым алгоритмом. При проведении анализа также оценивают рациональность построения схемы и возможность её упрощения за счет сокращения количества используемых элементов.

Задача анализа комбинационных ДУ заключается в нахождении ФАЛ, описывающих функцию каждого выхода исследуемого устройства. Отыскание такой ФАЛ становится возможным благодаря тому, что каждому логическому элементу схемы можно поставить в соответствие определённую логическую функцию. Данное соответствие обеспечивает однозначность схемной реализации ДУ и его математического описания.

Реализуемая ДУ функция АЛ обычно записывается в аналитическом виде, формируемом путём поэтапного описания схемы анализируемого ДУ. Для устройств, построенных на бесконтактных логических элементах, результирующая ФАЛ находится последовательной подстановкой функций выхода отдельных элементов вместо аргументов в функции, которые реализуются другими элементами схемы.

На основании полученного при описании схемы аналитического выражения может быть составлена таблица истинности исследуемой функции. Для большей наглядности при проведении исследований анализируемая функция также может быть записана в карту Карно. В некоторых случаях ФАЛ вместо аналитического выражения сразу удобно задавать в виде таблицы истинности или карты Карно. При таком способе получения ФАЛ значения, принимаемые функцией на каждом наборе аргументов, вычисляются непосредственно на основании схемы анализируемого устройства.

Задачу анализа рассмотрим на примере схемы (рис. 3.1), реализованной на контактах реле и управляющей включением лампочки Y (рис. 3.1, а).

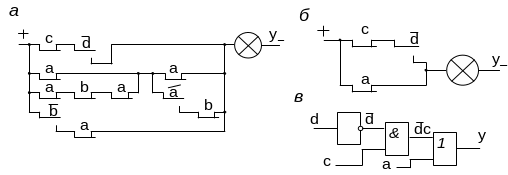
Рис. 3.1. Схема анализируемого дискретного устройства

Представленная схема (рис. 3.1, а) может быть описана функцией АЛ следующего вида:

. (3.1)

С целью оценки рациональности построения схемы и возможности её упрощения проведём минимизацию функции Y:

Анализ полученной в результате минимизации функции Y позволяет сделать вывод о нерациональности построения исходной схемы, возможности её существенного упрощения и сокращения количества используемых контактов реле (рис. 3.1, б). С помощью ФАЛ, полученной при минимизации, можно легко проанализировать функционирование схемы, определить соответствующие горению лампочки наборы аргументов, характеризующие состояния реле.

Целью синтеза комбинационной схемы является построение принципиальной схемы разрабатываемого ДУ по заданной функции. Поэтому задача синтеза ДУ является обратной по отношению к задаче, решаемой при выполнении анализа. Например, если задана функция Y, определяемая в соответствии с (3.1), то можно синтезировать реализующую эту функцию комбинационную схему (см. рис. 3.1, а). Однако построенная на основании формулы (3.1) схема ДУ будет содержать избыточное число контактов и, следовательно, не будет соответствовать оптимальной реализации функции Y. Поэтому при синтезе решается не только задача построения принципиальной схемы ДУ, но и задача определения структуры устройства, которая обеспечивает наиболее простую по количеству используемых элементов, а следовательно, и по надёжности функционирования и стоимости схемную реализацию (рис. 3.1, б).

В процессе выполняемого при синтезе ДУ логического проектирования структуры комбинационной схемы обычно решается задача минимизации определяющих данную схему функций АЛ, а также задача реализации разрабатываемого устройства, с использованием определённой элементной базы. Например, после выполнения минимизации функция Y может быть реализована не только релейно-контактной схемой (рис. 3.1, б), но и с помощью бесконтактных логических элементов (рис. 3.1, в).

Синтез комбинационной схемы начинается с определения используемых входных переменных и функций выхода проектируемого ДУ [1]. С помощью таблицы истинности или карт Карно задают значения, определяющие требуемые состояния выходов разрабатываемого ДУ на каждом наборе переменных. На следующем этапе синтеза выполняют минимизацию функций выхода, используя один из рассмотренных в подразд. 2.6 математических методов. После минимизации полученные функции представляют в базисе, обеспечивающем реализацию схемы синтезированного ДУ при использовании требуемой элементной базы.