2.6.3. Минимизация функций ал методом Квайна

Метод Квайна базируется на разложении ФАЛ на простые импликанты, осуществляемом путём последовательного применения к ДСНФ функции операций неполного склеивания (2.12) и элементарного поглощения (2.10). Определим понятие импликанты, минимизируемой ФАЛ.

Функция является импликантой минимизируемой функции , если на всех наборах аргументов на которых функция  равна единице, функция f также принимает единичное значение [1, 5]. Простой импликантой функции f называется любое элементарное произведение: , являющееся импликантой этой функции, при выбрасывании из которого любого сомножителя оно перестаёт быть импликантой функции f.

Дизъюнкция любого множества импликант одной и той же ФАЛ также является импликантой этой функции. Дизъюнкция всех входящих в какую либо полную систему импликант функции f совпадает с самой функцией f.

Для нахождения системы простых импликант минимизируемая функция представляется в дизъюнктивной совершенно нормальной форме. Выполняемые при переходе от ДНФ к ДСНФ преобразования рассмотрим на примере функции

.

С целью получения ДСНФ данной функции умножим каждое элементарное произведение на дизъюнкцию (равную единице) отсутствующей в данном произведении буквы и её отрицание. В результате такого преобразования от функции перейдём к функции

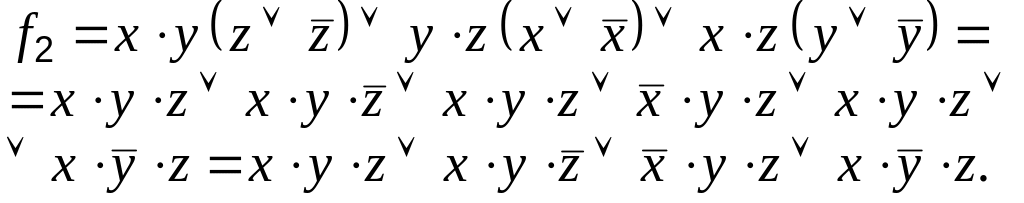
Функция после соответствующего преобразования представляет собой ДСНФ функции . Очевидно, что процесс перехода от к обратим. Для осуществления данного перехода можно использовать операцию склеивания, выполняемую на основании формулы

.

Однако применение операции склеивания приводит к исключению из конституент переменных, которые в дальнейшем могли бы использоваться для склеивания с другими конституентами единицы. Поэтому вместо операции склеивания целесообразно использовать операцию неполного склеивания, выполняемую в соответствии с выражением

.

Применение данной операции позволяет использовать для повторного склеивания уже подвергавшиеся склеиванию члены. Когда дальнейшее склеивание становится невозможным, приступают к удалению уже подвергавшихся склеиванию конституент единицы. Удаление осуществляют операцией элементарного поглощения:

.

В целях исключения возникновения ошибок операции неполного склеивания и элементарного поглощения необходимо осуществлять в соответствии с алгоритмом Квайна [1], [5], [11], [13], предусматривающим следующую последовательность преобразований минимизируемой функции:

1. запись функции в форме ДСНФ;

2. переход от ДСНФ к ДНФ путём осуществления всех возможных склеиваний, образующих ДСНФ конституент единицы;

3. исключение уже подвергавшихся всем склеиваниям конституент единицы с помощью операции элементарного поглощения.

Применение алгоритма Квайна рассмотрим на примере минимизации функции:

,

которая уже представлена в ДСНФ. С целью минимизации функции последовательно применяем операцию неполного склеивания к первому и второму, первому и третьему и первому и четвёртому элементарному произведению:

.

После осуществления всех возможных в данном случае склеиваний преобразуем функцию, используя операцию элементарного поглощения

.

После выполнения всех предусмотренных алгоритмом Квайна преобразований получаем разложение ФАЛ на простые импликанты, входящие в полную систему импликант функции .

Применение алгоритма Квайна в рассмотренном виде довольно трудоёмко в связи с необходимостью записи и сохранения большого количества конституент единицы. Поэтому при использовании данного метода для минимизации функций с большим количеством аргументов появляется вероятность возникновения ошибок. С целью упрощения использования метода Мак-Класки предложено более удобное оформление алгоритма Квайна, которое в основном и используется при минимизации ФАЛ с большим количеством переменных.