2.5.2. Понятие базиса и его выбор при реализации логических схем

Базисом называют функционально полную систему ФАЛ. Учитывая, что каждая функция функционально полной системы реализуется определённым логическим элементом, то минимальный набор логических элементов, обеспечивающий реализацию любой функции функционально полной системы, называется функционально полным набором. Для представления функций АЛ наиболее удобным и часто используемым является базис, содержащий конъюнкцию, дизъюнкцию и отрицание, т. е. функции "И", "ИЛИ", "НЕ". Данный набор функций называют основной функционально полной системой ФАЛ.

Выбор данного набора ФАЛ в качестве основного объясняется использованием при записи логического выражения операций дизъюнкции, конъюнкции и отрицания переменных. Записанное с помощью таких операций выражение всегда может быть реализовано логической схемой, построенной с использованием элементов "И", "ИЛИ", "НЕ".

Реализация функций f₀, f₁₅, f₃, f₅, представляющих собой константы "0", "1" и повторение переменных а, b через функции основной функционально полной системы, с технической точки зрения нецелесообразна. Реализацию данных функций удобно осуществлять путём подключения входа элемента к одному из полюсов источника питания или выходу устройства, используемого для формирования соответствующих переменных а, b. Поэтому при построении логической схемы ДУ совместно с функциями основной функционально полной системы также используют функции f₀, f₁₅, f₃, f₅ (см. табл. 2.3).

Наряду с основной функционально полной системой ФАЛ при схемной реализации ДУ часто используют и другие функционально полные системы. Наибольшее распространение получили базисы, образованные с использованием функций "И-НЕ", "ИЛИ–НЕ", каждая из которых (сама по себе) образует самостоятельный базис.

Примеры реализации на контактах реле и на бесконтактных логических элементах ряда функций, входящих в некоторые, наиболее часто используемые базисы, представлены в табл. 2.4.

Таблица 2.4

Реализация функций, входящих в наиболее часто используемые базисы

Реализуемая ФАЛ логическая операция	Обозначение при реализации
	на контактных реле	на бесконтактных логических элементах
Инверсия “НЕе”
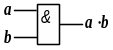
Конъюнкция “И”
Дизъюнкция “ИЛИ”
Отрицание конъюнкции “И–НЕ”
Отрицание дизъюнкции “ИЛИ–НЕ”

В процессе реализации ФАЛ на элементах, входящих в состав определённой серии микросхем, часто приходится решать задачу преобразования ФАЛ с целью представления её в функциях другой функционально полной системы. Для перехода между наиболее часто используемыми базисами применяется закон двойного отрицания и закон двойственности. Приведение ФАЛ, представленной в функциях "И", "ИЛИ", "НЕ" основной функционально полной системы, к базисам "И–НЕ" и "ИЛИ–НЕ иллюстрируют следующие примеры.

В базисе "И", "ИЛИ", "НЕ"

_.

В базисе "И–НЕ"

_.

В базисе "ИЛИ–НЕ"

_.

Используя набор логических элементов, образующих базис, можно реализовать любую логическую структуру ДУ. Однако стремление к сокращению количества применяемых элементов, как правило, обычно существенно усложняет схему логического устройства. Использование при построении электронных схем логических элементов, входящих в различные функционально полные наборы функций АЛ, обеспечивает более простую схемную реализацию разрабатываемого устройства.