2) Закон Био – Савара – Лапласа.

Любой элемент dl проводника с током I создаёт в окружающем пространстве на расстоянии r под углом магнитное поле индукцией

Б13.1) Работа электростатического поля при перемещении зарядов.

При перемещении заряда в электростатическом поле, кулоновские силы совершают работу. Пусть заряд q₀0 перемещается в поле заряда q0. На q₀ действует кулоновская сила . Приперемещении заряда. , где - угол между векторами и . Величина является проекцией вектора на направление силы .⇒ , . Полная работа по перемещению заряда , где r₁ и r₂ - расстояния заряда q до точек С и В.

Потенциал электростатического поля.

Отношение потэнергии заряда к величине заряда.

2) Работа по перемещению проводника с током в магнитном поле.

Работа при перемещении проводника с током и контура с током в магнитном поле. Работа по перемещению проводника с током равна произведению тока на магнитный поток пересечённый движущимся проводником.

Б14.1) Свободные и связанные заряды.

Свободные заряды – заряженные частицы одного знака, способные перемещаться под действием электрического поля.

Связанные заряды – разноимённые заряды, входящие в состав атомов, которые не могут перемещаться под действием электрического поля независимо друг от друга.

Связь вектора поляризованности с плотностью связанных зарядов.

Нормальная составляющая вектора поляризованности равна поверхностной плотности связанного заряда.

Теорема Гаусса для вектора поляризованности.

Поток вектора Р сквозь любую замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объёме, охватываемом поверхностью интегрирования S:

2) Поле на границе раздела магнетиков.

Для определения условий на границе двух однородных магнетиков используют теорему Гаусса для вектора  и теорему о циркуляции вектора

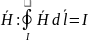
Условия для вектора : ; ;

Условия для вектора : , где – проекция вектора на нормаль к контуру. Если на границе тока проводимости нет , то тангенсальная составляющая вектора не испытывает скачка:

Б15. 1) Поле на границе раздела диэлектриков.

Изменение величины нормальной составляющей вектора смещения равно плотности стороннего заряда.

Изменение величины нормальной составляющей вектора поляризованности на границе раздела диэлектриков равно с обратным знаком поверхностной плотности связанного заряда.

Если сторонних зарядов на границе раздела нет, то

2) Расчёт магнитного поля соленоида.

Циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной на сумму токов охватываемых этим контуром. Соленоид

Б16. 1) Поток вектора напряженности электрического поля.

Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называют потоком вектора напряженности электрического поля сквозь эту поверхность E_n — нормальная к площадке компонента вектора напряженности.

Теорема Гаусса в интегральной и дифференциальной формах в вакууме и её применение для расчёта электростатических полей.

Поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охваченных этой поверхностью, делённой на . Если ввести функцию объёмного распределения электрического заряда  x, y,z , такую, что и воспользоваться теоремой Остроградского-Гаусса , то из равенства получим дифференциальную форму теоремы Гаусса: .

Поле равномерно заряженного цилиндра.

Поток вектора напряжѐнности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгеброической сумме заключенных внутри этой поверхности зарядов делѐнной на 0 . Цилиндр