Б1.1) Вектор электрического смещения. В однородном изотропном диэлектрике . Введем величину - относительную диэлектрическую проницаемость вещества. . Введем новый вектор D который называется вектором электрического смещения или вектором электрической индукции. Следовательно, из теоремы Гаусса для вектора напряжѐнности электрического поля E следует теорема Гаусса для вектора электрического смещения D: .

Теорема Гаусса для вектора электрического смещения. поток вектора электрического смещения через замкнутую поверхность, равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью:

2) Плотность энергии магнитного поля. Энергия магнитного поля проводника с током . Плотность энергии вычисляют как ω = dW/dV или для однородного поля ω = W/V. .

Б2.1) Электроёмкость проводников и конденсаторов.

Емкость конденсатора: ; Емкость уединенного проводника: ; Шар R: . Плоский: . Цилиндрический: Сферический:

Вычисление ёмкости сферического проводника. Сообщим уединённому сферическому проводнику радиуса R заряд Q. Потенциал проводника станет равным ; , .

2) Магнитная восприимчивость и магнитная проницаемость вещества. Величину , называют магнитной проницаемостью. Это безразмерная характеристика вещества. Увеличение потока Ф в раз означает, что магнитная индукция в сердечнике во столько же раз больше, чем в вакууме при том же токе в соленоиде. Следовательно, можно записать, что: , где - магнитная индукция поля в вакууме.

Обычно вектор намагниченности ( ) связывают с вектором напряженности в каждой точке магнетика: , где - магнитная восприимчивость, безразмерная величина.

Б3.1) Работа электростатического поля при перемещении зарядов.

При перемещении заряда в электростатическом поле, кулоновские силы совершают работу. Пусть заряд q₀0 перемещается в поле заряда q0. На q₀ действует кулоновская сила . Приперемещении заряда. , где - угол между векторами и . Величина является проекцией вектора на направление силы .⇒ , . Полная работа по перемещению заряда , где r₁ и r₂ - расстояния заряда q до точек С и В.

Циркуляция вектора напряженности Называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L. (если замкн, то =0).

2) Принцип суперпозиции магнитных полей. если магнитное поле создано несколькими проводниками с токами, то

Поле кругового тока. Возьмем проводник, согнутый по кругу, и пропустим по нему ток. Направление поля кругового тока можно определить, пользуясь "правилом буравчика". Напряженность магнитного поля кругового тока в центре определяется по формуле: . Индукция магнитного поля кругового тока:

Б4.1) Поток вектора напряженности электрического поля.

Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называют потоком вектора напряженности электрического поля сквозь эту поверхность 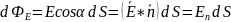E_n — нормальная к площадке компонента вектора напряженности.

Теорема Гаусса в интегральной и дифференциальной формах в вакууме и её применение для расчёта электростатических полей.

Поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охваченных этой поверхностью, делённой на . Если ввести функцию объёмного распределения электрического заряда  x, y,z , такую, что и воспользоваться теоремой Остроградского-Гаусса , то из равенства получим дифференциальную форму теоремы Гаусса: .

Поле равномерно заряженной плоскости. бесконечная плоскость заряжена равномерно с поверхностной плотностью заряда  (=dQ/dS). Выделим площадку S и окружим ее цилиндрической замкнутой поверхностью с основанием, параллельным плоскости. Так как линии вектора Е перпендикулярны плоскости и параллельны образующим цилиндра, то полный поток через цилиндрическую замкнутую поверхность равен сумме потоков лишь через два ее основания: . Согласно теореме Остроградского-Гаусса , Приравняв правые части для N, получим

2) Проводники с током в магнитном поле. Если внести проводник с током в магнитном поле, то в результате сложения магнитных полей магнита и проводника произойдет усиление магнитного поля с одной стороны проводника и ослабление с другой стороны. В результате действия двух магнитных полей произойдет искривление магнитных линий, и они, стремясь сократиться, будут выталкивать проводник. Сила называется электромагнитной. Направление по «правилу левой руки».

Закон Ампера. Из закона: параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются.

Б5.1) Энергия системы неподвижных зарядов.

2)Поток вектора магнитной индукции.

Пронизывающий площадку S - величина, равная: . в веберах (Вб). Число линий магнитной индукции, проходящих сквозь данную поверхность.

Теорема Гаусса для магнитного поля.

Для произвольной замкнутой поверхности S поток вектора индукции : . Если число линий магнитной индукции, входящих внутрь объема, равно числу линий, выходящих из этого объема, суммарный поток Ф_B вектора B через произвольную замкнутую поверхность S равен нулю: .

Б6.1) Поток вектора напряженности электрического поля.

Число силовых линий, пронизывающих некоторую поверхность, расположенную в электрическом поле, называют потоком вектора напряженности электрического поля сквозь эту поверхность E_n — нормальная к площадке компонента вектора напряженности.

Теорема Гаусса в интегральной и дифференциальной формах в вакууме и её применение для расчета электростатических полей.

Поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охваченных этой поверхностью, делённой на . Если ввести функцию объёмного распределения электрического заряда  x, y,z , такую, что и воспользоваться теоремой Остроградского-Гаусса , то из равенства получим дифференциальную форму теоремы Гаусса: .

2) Электромагнитная индукция.

Явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, проходящего через него.

Закон Фарадея. Правило Ленца. Согласно закону электромагнитной индукции Фарадея: Знак «минус» в формуле отражает правило Ленца: Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Б7.1) Связь напряженности и потенциала.

;

Уравнение Пуассона. Уравнение Пуассона - эллиптическое дифференциальное уравнение в частных производных, которое описывает электростатическое поле: где  — оператор Лапласа, или лапласиан. В трёхмерной декартовой системе координат уравнение принимает форму: 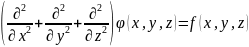. Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

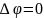
2) Теорема о циркуляции вектора намагниченности ЦВН по произвольному замкнутому контуру равна сумме микротоков, сцепленных с этим контуром.

Б8.1) Электроёмкость проводников и конденсаторов.

Емкость конденсатора: ; Емкость уединенного проводника: ; Шар R: . Плоский: . Цилиндрический: Сферический:

Вычисление ёмкости плоского конденсатора.

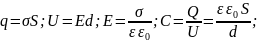
2) Магнитное поле в веществе.

Суперпозиция 2х полей: внутреннего ( ) и внешнего ( )

Молекулярные токи.

(Микротоки) Токи, обусловленные движением электронов в атомах, молекулах. В в-ве возникает собственное магнитное поле- намагниченность.

Намагниченность вещества. Вектор намагниченности

Магнитный момент единицы объема магнетика:

Б9.1) Принцип суперпозиции и его применение к расчёту поля системы неподвижных зарядов.

Вектор напряжённости поля, создаваемого системой неподвижных точечных зарядов, равен векторной сумме напряжённостей полей, создаваемых каждым из зарядов в отдельности: 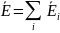. Это следует из того, что силы складываются как векторы: , поэтому

Электрическое поле диполя. ЭД – сов-ость = по величине, но противоположных по знаку двух точечных зарядов –q и +q, сдвинутых друг относительно друга на некоторое расстояние. Пусть   – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор называется дипольным моментом, вектор  – плечом диполя. В соответствии с принципом суперпозиции для вектора напряженности, напряженность ЭП в точечном диполе равна