7.1.1. Правило максимизации полезности
Допустим, потребитель тратит определенную часть дохода на товары Х и Y. На какое количество товаров Х и Y он должен предъявить спрос, чтобы максимизировать для себя полезность этих товаров?
Допустим, вначале потребитель оценивает предельную полезность товара Х больше, чем Y. Тогда он начнет увеличивать потребление товара Х и сокращать Y. Но по закону убывающей предельной полезности при увеличении потребления Х – его предельная полезность начнет снижаться, а у Y – увеличиваться. В конце концов должно установиться равенство оценок предельных полезностей товаров Х и Y. Теперь потребитель не будет тратить ни на рубль больше на товар Х, и ни на рубль меньше на товар Y.
Это будет идеальное положение, когда человеку невыгодно менять структуру потребления, т.к. любое изменение приведет к ухудшению благосостояния (это второй закон Госсена).
Т.о. правило максимизации полезности: потребитель так должен израсходовать свой доход, чтобы отношение предельной полезности к цене было одинаковым для всех товаров, при этом доход должен быть истрачен полностью:
MUx/Px = MUY/PY
Отношение MU/P показывает величину предельной полезности в расчете на 1 затраченный рубль.
Рассмотрим пример: пусть доход потребителя = 36 руб. Цена товара Х = 6 руб., Y = 8 руб. Общая полезность от потребления этих товаров дана в таблице. На какое количество товаров должен предъявить спрос покупатель, чтобы получит максимум полезности?
-
Единица товара
1
2
3
4
5
Ux
18
30
38
42
44
UY
32
56
72
80
84
Сначала найдем предельные полезности, а затем их в расчете на 1 рубль для обоих товаров:
-
Единица товара
1
2
3
4
5
МUx
18
12
8
4
2
МUx/Рх
3
2
4/3
2/3
1/3
МUY
32
24
16
8
4
MUY/Ру
4
3
2
1
1/2
Получается несколько комбинаций, но лучшая, где он истратит и все деньги:
2 Х и 3 Y.
7.2. Теория потребительского выбора
Данная теория отрицает возможность количественного измерения полезности. Но также пытается найти оптимальную комбинацию двух товаров Х и Y, которая принесла бы потребителю наибольшее удовлетворение. Выбор потребителя зависит от его желания и возможностей, поэтому их необходимо совместить.
Линия бюджетного ограничения (бюджетная линия) показывает различные комбинации двух товаров, которые могут быть приобретены при фиксированной величине денежного дохода и при данном уровне цен на эти товары (т.е. отражает возможности потребителя) (Рис. 7.2).
Рис. 7.2. Бюджетная линия
Уравнение бюджетного ограничения:
I = PxQx+PYQY, если переписать относительно QY – зависимость линейная, наклон отрицательный.
где I – величина дохода потребителя
РХ – цена товара Х
РY – цена товара Y
где QХ – объем спроса на товар Х
QY - объем спроса на товар Y
Расположение бюджетной линии зависит от дохода и изменения цен:
- если доход потребителя увеличится, то увеличится и количество наборов, доступных покупателю, и линия сдвинется вправо;
- при уменьшении дохода, количество наборов снизится, линия сдвинется влево;
- снижение цен товаров Х и Y сместит линию вправо и наоборот;
- снижение цены товара Х (при неизменной Y) приведет к тому, что на тот же доход можно купить больше товара Х: нижняя часть линии сдвинется вправо;
- снижение цены Y (при неизменной Х) сдвинет верхнюю часть линии вверх.
Таким образом, бюджетная линия отражает объективные факторы, но есть еще субъективные рыночные факторы, которые влияют на поведение потребителя – вкусы и предпочтения. Они анализируются с помощью кривых безразличия.
Кривая безразличия – это линия, соединяющая все точки наборов двух благ, имеющих для потребителя одинаковую общую полезность. Т.е. потребителю безразлично, какой набор товаров Х и Y он выберет.
Пример: потребитель безразлично относится к четырем наборам (Таблица 7.2).
Таблица 7.2
-
наборы
Кол-во персиков (Qy)
Кол-во киви (Qх)
А
7
4
B
5
5
C
4
6
D
3
8
По данным таблицы построим кривую безразличия (Рис. 7.3):
Рис. 7.3. Кривая безразличия потребителя
Каждая ее точка представляет набор с одинаковой полезностью. Но если мы увеличим количество персиков и киви, то перейдем на другую кривую безразличия, которая будет дальше от начала координат. И любой ее набор будет лучше, чем на первой кривой.
В своей совокупности все кривые безразличия представляют собой карту безразличия – она обеспечивает ранжирование наборов потребительских товаров: от наиболее до наименее предпочтительных (отражает желания потребителя) (Рис. 7.4).
Рис. 7.4. Карта кривых безразличия
По кривой безразличия можно рассчитать, каким количеством персиков потребитель готов пожертвовать ради получения дополнительных киви (сначала – 2 персиками, затем 1, потом 0,5). Т.е. по мере продвижения вниз по кривой, покупатель готов отказаться от все меньшего количества персиков – поэтому кривая имеет выпуклую форму, т.к. потребители получают все меньше удовольствия по мере большего потребления товара.
Количество одного товара (Y), которое потребитель согласен потерять с тем, чтобы получить дополнительную единицу другого товара (Х) и оказаться на том же уровне полезности, называется предельной нормой замены (товара Y товаром Х):
MRS = -
Знак «-» вводится для того, чтобы предельная норма замены одного товара другим была положительной величиной (т.к. числитель всегда отрицательный) (в нашем примере MRS = 2; 1; 0.5 - снижается)
Но бывают случаи, когда предельная норма замены не снижается:
- на взаимозаменяемые товары, когда потребитель в равной степени будет жертвовать определенным количеством одного товара для приобретения 1 единицы другого (кривая безразличия примет форму как бюджетная линия);
- для взаимодополняемых товаров, когда потребление одного невозможно без другого (MRS = 0), а кривая безразличия пройдет под углом 900 (Рис. 7.5)
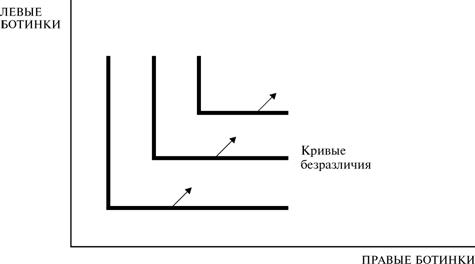
Рис. 7.5. Кривая безразличия взаимодополняемых товаров
Теперь совместим желания и возможности потребителя и найдем такой набор товаров, который принесет наибольшую полезность (рис. 7.6).
Рис. 7.6. Карта кривых безразличия и бюджетная линия. Равновесное положение
Равновесное положение потребителя достигается в точке, в которой бюджетная линия касается наиболее высокой из всех достижимых кривой безразличия (точка В2). В этой точке наклон кривой безразличия равен наклону бюджетной линии. Так как наклон кривой безразличия отражает предельную норму замены одного товара другим (MRS), а наклон бюджетной линии – отношение цены товара Х к цене товара Y, то равновесие потребителя достигается при условии, что предельная норма замены одного товара другим равна обратному отношению цен:
MRS=Рх/Рy