
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
- •«Введение в анализ и дифференциальное исчисление функции одной переменной»
Задания и варианты контрольной работы №2 по теме:
«Введение в анализ и дифференциальное исчисление функции одной переменной»
1. Построив эскиз графика основной элементарной функции, с помощью последовательных преобразований изобразить эскиз графика функции y.
2. Вычислить пределы, не используя правило Лопиталя. (Рекомендация – использовать замену на эквивалентные функции).
3. Вычислить производные.
4. Сравнить функции α(x) и β(x); φ(x) и ψ(x); f(x) и g(x) при x→x0.
(Рекомендация – использовать правило Лопиталя).
5. Провести исследование и построить графики функций.
Вариант 1
1.
a).
![]() б).
б).
![]() в).
в).
![]()
2.
а).
![]() б).
б).
![]() в).
в).
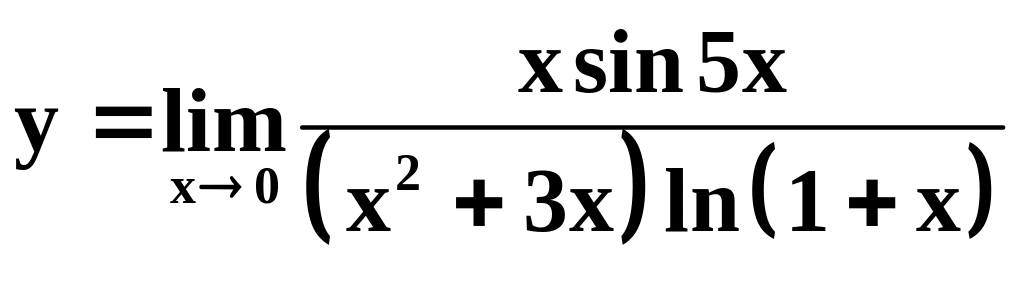
3.
а).
![]() б).
б).
![]() в).
в).
![]()
4.
а).
![]() ,
,
![]() ,
,
![]()
б).
![]() ,
,
![]() ,
,
![]()
в).
![]() ,
,
![]() ,
,
5.
а).
![]() б).
б).
![]()
Задания и варианты контрольной работы №2 по теме:
«Введение в анализ и дифференциальное исчисление функции одной переменной»
1. Построив эскиз графика основной элементарной функции, с помощью последовательных преобразований изобразить эскиз графика функции y.
2. Вычислить пределы, не используя правило Лопиталя. (Рекомендация – использовать замену на эквивалентные функции).
3. Вычислить производные.
4. Сравнить функции α(x) и β(x); φ(x) и ψ(x); f(x) и g(x) при x→x0.
(Рекомендация – использовать правило Лопиталя).
5. Провести исследование и построить графики функций.
Вариант 2
1.
a).
![]() б).
б).
![]() в).
в).
![]()
2.
а).
![]() б).
б).
![]() в).
в).
![]()
3.
а).
![]() б).
б).
![]() в).
в).
![]()
4.
а).
![]() ,
,
![]() ,
,
б).
![]() ,
,
![]() ,
,
![]()
в).
![]() ,
,
![]() ,
,
5.
а).
![]() б).
б).
![]()
Задания и варианты контрольной работы №2 по теме:
«Введение в анализ и дифференциальное исчисление функции одной переменной»
1. Построив эскиз графика основной элементарной функции, с помощью последовательных преобразований изобразить эскиз графика функции y.
2. Вычислить пределы, не используя правило Лопиталя. (Рекомендация – использовать замену на эквивалентные функции).
3. Вычислить производные.
4. Сравнить функции α(x) и β(x); φ(x) и ψ(x); f(x) и g(x) при x→x0.
(Рекомендация – использовать правило Лопиталя).
5. Провести исследование и построить графики функций.
Вариант 3
1.
a).
![]() б).
б).
![]() в).
в).
![]()
2.
а).
![]() б).
б).
 в).
в).
![]()
3.
а).
![]() б).
б).
 в).
в).
![]()
4.
а).
![]() ,
,
![]() ,
,
![]()
б).
![]() ,
,
![]() ,
,
![]()
в).
![]() ,
,
![]() ,
,
5.
а).
![]() б).
б).
![]()
Задания и варианты контрольной работы №2 по теме:
«Введение в анализ и дифференциальное исчисление функции одной переменной»
1. Построив эскиз графика основной элементарной функции, с помощью последовательных преобразований изобразить эскиз графика функции y.
2. Вычислить пределы, не используя правило Лопиталя. (Рекомендация – использовать замену на эквивалентные функции).
3. Вычислить производные.
4. Сравнить функции α(x) и β(x); φ(x) и ψ(x); f(x) и g(x) при x→x0.
(Рекомендация – использовать правило Лопиталя).
5. Провести исследование и построить графики функций.
Вариант 4
1.
a).
![]() б).
б).
![]() в).
в).
![]()
2.
а).
![]() б).
б).
![]() в).
в).

3.
а).
![]() б).
б).
![]() в).
в).
![]()
4.
а).
![]() ,
,
![]() ,
,
б).
![]() ,
,
![]() ,
,
в).
![]() ,
,
,
,
5.
а).
![]() б).
б).
![]()
Задания и варианты контрольной работы №2 по теме:
