Метод рядів Тейлора.

Цей метод є еталонним методом, за яким порівнюють точність різних чисельних методів при розв‘язанні задачі Коші.

Теорема Тейлора: Припустимо, що і що функцію y(x) можна розкласти в ряд Тейлора порядку n у околі фіксованої точки х = х_k [x₀, x_n] :

(1.17)

де інтеграл наближено представлений рядом Тейлора:

(1.18)

У формулі 1.18 є (j-1)-ю похідною по (х_k) функції f. Отримаємо формулу для похідної за допомогою рекурентної процедури:

(1.19)

де є частинними похідними по відповідним змінним.

У загальному виді:

(1.20)

де - диференційний оператор. При розв‘язанні задачі Коші ітерація Тейлора має вигляд:

(1.21)

де , . Остаточна похибка методу Тейлора має порядок . Точність методу Тейлора залежить від кількості елементів ряду. Для n = 4 і для кроків h та h/2 похибка обчислень:

(1.22)

Методи Рунге-Кутта.

Ці методи виводяться з відповідних методів Тейлора таким чином, щоб остаточна загальна помилка методів не перевищувала порядку О(h ^N). Методи були виведені для того, щоб на кожному кроці виключити необхідність підрахунку похідних вищих порядків.

Методи Рунге-Кутта будуються для будь-яких порядків N, що обумовлені точністю. Найчастіше застосовується метод Рунге-Кутта 4-го порядку (N=4). Він дає досить малу помилку при невеликій кількості розрахунків і не складний для програмування. Метод оснований на обчисленні наступного значення за попереднім по формулі:

(1.11)

де k₁, k₂, k₃, k₄ – коефіцієнти, що розраховуються за формулами:

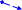(1.12)

Р унге і Кутт отримали систему рівнянь, що має локальну похибку відсікання порядку О(h⁵):

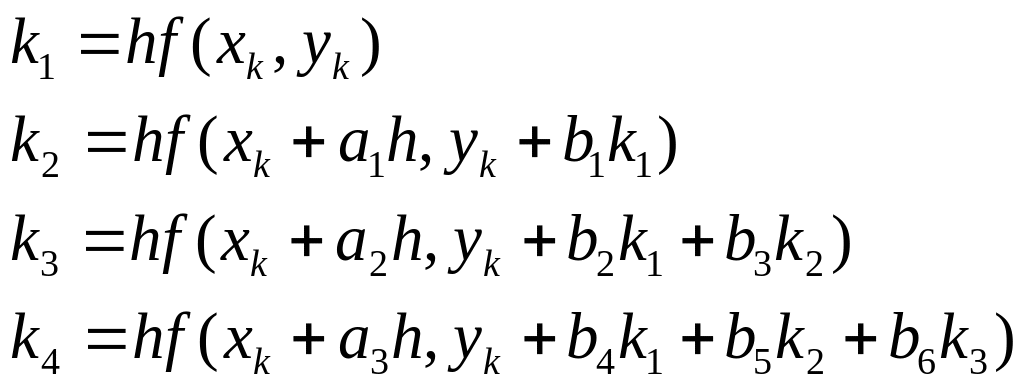
(1.13)

Отримані 11 рівнянь вміщують 13 змінних, тому для їх розв’язання потрібні 2 додаткові умови. Такими умовами найчастіше є:

(1.14)

За таких умов розв’язками системи рівнянь будуть:

Підставляючи значення (1.13) та (1.14) в початкове рівняння (1.11) отримаємо формулу для стандартного методу Рунге-Кутта 4-го порядку:

, (1.15)

д е

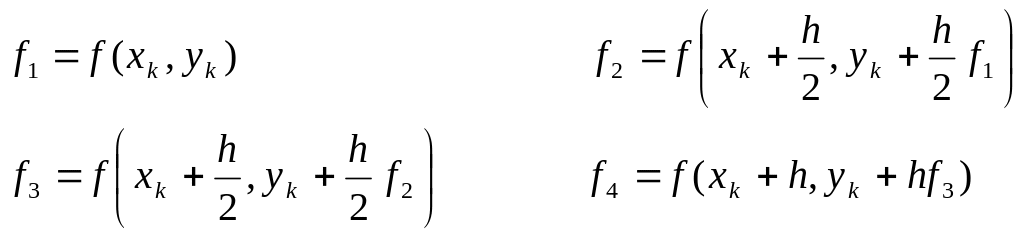
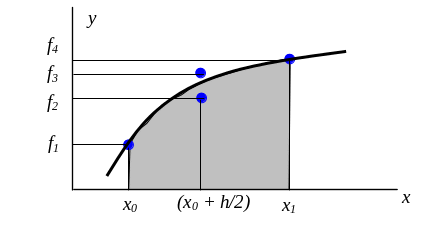
Рис. 2. Наближення інтегралу за методом Рунге-Кутта 4-го порядку.

Накопичена похибка в методі Рунге-Кутта складається з елементарних похибок, що утворюються на кожному кроці Дана похибка методу розраховується за формулою:

. (1.16)

Наприклад: задана функція y = (x-y)/2 на інтервалі [0; 3] з початковою умовою у(0)=1. Виберемо крок h = 0,25. На першій ітерації підрахуємо значення коефіцієнтів f₁, f₂, f₃, f₄ і чергове значення y₁:

Всі інші значення на інтервалі [0; 3] розраховуються аналогічно, не застосовуючи операцію диференціювання.

12