2. Игры с природой

2.1 Понятие игры с природой

Рассмотренные выше матричные и биматричные игры и методы их решения предполагали многократные повторения решений с некоторыми вероятностями (частотами) применения выбранных стратегий игроками. На практике при решении экономических задач, которые сводятся к игровым моделям, количество принимаемых управленческих решений ограничено, а нередко вообще принимается однократно в условиях неопределенности и риска.

В игровых задачах, которые моделирую экономические процессы с такого рода неопределенностью, принятие решения зависит от состояния объективной действительности, которую принято называть «природой». Следовательно, в игре с природой осознанно действует только один игрок, лицо принимающее решение. Второй игрок - природа, которая осознанно против первого игрока не действует, принимая то или иное состояние произвольным образом, конкретных целей в игре не преследует и безразлична к результату игры. Поэтому термин «природа» характеризует некоторую реальность – политика, финансы, промышленность, сельское хозяйство и т.п., которая в задачах будет провялятся в конкретных формах.

Математическая модель игр с природой следующая. Пусть игрок А (ЛПР) имеет m стратегий A_i, i=1,…,m, а природа Q может находится в одном из n возможных состояний Q_j, j=1,…,n, которые можно рассматривать как ее стратегии. Тогда платежную матрицу игры с природой можно представить в виде, аналогичном платежной матрицы А = (a_ij)_mxn, или

	Q1	Q2	…	Qn
A1	a11	a12	…	a1n
A2	a21	a21	…	a2n
…	…	…	…	…
Am	am1	am2	…	amn

Здесь a_ij – выигрыши игрока А при выборе стратегии А_i и при состоянии природы Q_j. Матрица игры с природой содержательно отличается от платежной матрицы антагонистической игры тем, что элементы столбцов данной матрицы не являются проигрышами природы при соответствующих ее состояниях, а это оценка эффективности стратегии ЛПР при данных состояниях природы.

3.2 Доминирование (мажорирования) в играх с природой.

В игре с природой также можно доминировать (мажорировать) стратегии игрока А (ЛПР), что позволяет уменьшить размерность платежной матрицы. При этом доминировать стратегии второго игрока Q, природы недопустимо, так как природа не стремится к выигрышу в игре, а действует неосознанно.

риска.

Задача. Дана платежная матрица А игры с природой размерности 4х4.

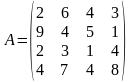
Провести операции доминирования с целью уменьшить размерность матрицы.

Решение.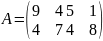

Стратегия А₄ доминирует А₁ и А₃, поэтому их можно исключить и размерность новой матрицы будет (2х4) с элементами стратегий А₂ и А₄.

3.3 Игры с природой в условиях полной неопределенности.

Рассмотрим игру с природой, в которой вероятности состояний природы Q_j неизвестны и отсутствует возможность получения о них какой-либо статистической информации. В таких игровых моделях для нахождения наилучших решений используются следующие критерии: максимакса, Вальда, Сэвиджа и Гурвица.

1. Критерий максимакса.

Это критерий беспредельного оптимизма, максимизирующий максимальные выигрыши игрока принимающего решения для каждой его стратегии путем перебора всех состояний природы по формуле:

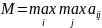(3.1)

Этим критерием пользуются не только оптимисты, но и игроки попавшие в безвыходное положение и пытающиеся получить максимальный выигрыш.