1.2.4 Матричные игры mx2.

Рассмотрим матричную игру размерности (m´2) с платежной матрицей

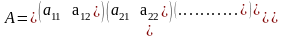
Положим, что эта матричная игра в чистых стратегиях решения не имеет, седловой точки – нет. Пусть смешанные стратегии игроков заданы

,

Тогда, следуя теореме , решение игры находится из второго уравнения (1.4):

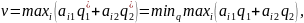
где i=1,…,m.

Для определения минимума по q функции

построим ее график состоящий из m прямых вида

,

на плоскости q0ν по следующему алгоритму:

1) на оси абсцисс Oq откладываем отрезок единичной длины;

2) на оси ординат (q=0) откладываем проигрыши при стратегии В₁ (a_i1), а на вертикальной линии (q=1) проигрыши при стратегии B₂ (a_i2) ;

3) строим линии стратегий A₁, A₂,…, A_m проходящие через точки:

(0,a_i1) и (1,а_i2), при i=1,…,m;

4) затем строим полигональную линию огибающую пучок этих линий сверху;

5) на огибающей находим вершину с минимальной ординатой;

6) абсцисса этой вершины есть вероятность q₂^* выбора оптимальной смешанной стратегии B₂ , тогда для стратегии B₁ имеем q₁^*=1- q₂^*, а

ордината этой вершины определяет цену игры ν^*.

Задача

Дана конечная матричная игра с платежной матрицей вида:

.

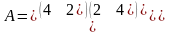Определить оптимальные стратегии игроков и цену игры.

Решение.

1) Решение в чистых стратегиях

	B1	B2	αi
A1	4	2	2
A2	2	4	2
A3	6	3	3
βj	6	4

Имеем,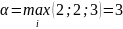 , . Так как α< β, игра не имеет решения в чистых стратегиях, т.к. седловой точки нет.

2) Решение в смешанных стратегиях.

Смешанные стратегии игроков

,

Строим график в системе координат qOν в соответствии с описанным выше алгоритмом.

Решение для игрока В.

_{Полигональная линия М}NC – верхняя огибающая, соответствующая верхней границе цены игры, т. е. наилучшим ситуациям для игрока В. Минимальное значение достигается в точке N, которая образуется пересечением линий, соответствующих стратегиям А₃ и А₂ игрока А. Абсцисса точки N соответствует вероятности q₂^* применения игроком B чистой стратегии B₂, а q₁^*=1- q₂^*– вероятности применения игроком B чистой стратегии B₂. Ордината точки С – цена игры ν^*. Оптимальное решение для игрока А, следующее:

, ν^* = 18/5.

Оптимальное решение можно получить аналитически из решения системы двух линейных уравнений воспользовавшись формулами (1.6) заменяя в них элементы матрицы, соответственно: a₁₁, a₁₂, a₂₁, a₂₂ на a₂₁, a₂₂, a₃₁, a₃₂

Решение для игрока А.

Точка N является пересечением пары чистых стратегий A₂ и A_3. Следовательно, вероятности использования других стратегий равны нулю: p₁= 0. На графике p₂^* и p₃^* равны долям, на которые проекция точки N на ось ординат Oν делит отрезок ( a₃₁ a₂₁). Можно найти точные значения p₂^* и p₃^* из решения системы двух линейных уравнений соответствующих стратегиям A₂ и A_3.

Оптимальное решение для игрока A, следующее:

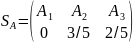, ν^* = 15/4.

Оптимальное решение можно получить аналитически из решения системы двух линейных уравнений воспользовавшись формулами (1.5) заменяя в них элементы матрицы, соответственно: a₁₁, a₁₂, a₂₁, a₂₂ на a₂₁, a₂₂, a₃₁, a₃₂.