1.1.2 Аффинное правило.

Пусть задана исходная платежная матрица А=(a_ij) размерности mxn. Аффинное преобразование - это линейное преобразование всех элементов матрицы А по формуле

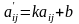
где k ≠ 0 и b –любые константы.

Решение матричной игры для платежной матрицы А^'=(a^'_ij) совпадает с решением для исходной платежной матрицы. Цену игры ν для исходной платежной матрицы можно найти из цены игры для преобразованной платежной матрицы ν^’, опираясь на аффинное правило по формуле

Задача. Задана платёжная матрица игры:

A =

Необходимо упростить матрицу игры.

1. Умножим каждый из элементов матрицы A на k = 0.001, получим:

2. К каждому элементу матрицы 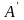прибавим b = 5, получим матрицу:

=

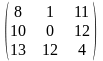
Таким образом, мы получили платёжную матрицу с положительными элементами и небольшими по абсолютной величине. Искать решение для платежной матрицы А^" проще, чем для исходной А.

1.2 Решение игр в смешанных стратегиях

Пусть платежная матрица А размерности (mxn) не имеет решения в чистых стратегиях, т.е. и седловая точка отсутствует.

Поиск решения игры в этом случае сводится к случайному применению чистых стратегий с определенными частотами. Такая сложная стратегия называется смешанной.

Смешанная стратегия игрока А задается m-мерным вектором вероятностей (частот) 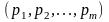, с которыми игрок применяет свои чистые стратегии

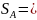
При этом .

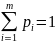Аналогично, смешанная стратегия игрока В это набор вероятностей (частот) определяемый n-мерным вектором

и .

Если мы окажемся в ситуации применения стратегий игроками в сочетании (A_i,B_j), то она будет реализована с вероятностью p_i.q_j, а выигрыш составит величину a_ij. Тогда средний выигрыш игрока А можно рассчитать как математическое ожидание:

,

где p и q вектора вероятностей стратегий игроков А и В.

Стратегии p^*=(p₁^*,p₂^*,…,p_m^*) и q^*=(q₁^*,q₂^*,…,q_m^*) называются оптимальными смешанными стратегиями игроков, если выполнены следующие соотношения

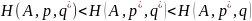(1.1)

Величина 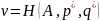называется ценой игры, а рассчитанные значения 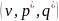решением матричной игры в смешанных стратегиях.

Необходимое и достаточное условие существования оптимального решения матричной игры в смешанных стратегиях определяется теоремой Д. Неймана. Методы решения матричных задач в смешанных стратегиях основываются на следующей теореме.

Теорема. Оптимальная смешанная стратегия p^* игрока А смешивается только из тех чистых стратегий A_i , (p_i^* 0), для которых выполнено равенство

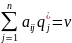(1.2)

В оптимальной смешанной стратегии q^* игрока В смешиваются только те стратегии В_j для которых выполнены равенства

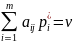(1.3)

Кроме того справедливы равенства

(1.4)

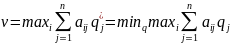
1.2.1 Аналитическое решение матричной игры 2х2.

Рассмотрим матричную игру размерности (2´2) с платежной матрицей

.

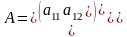Положим, что решение этой матричной игры в чистых стратегиях найти не удалось, седловой точки – нет. Пусть смешанные стратегии игроков заданы

,

Оптимальные стратегии p₁ и p₂ определим из решения системы уравнений(1.3):

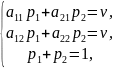
или получим

Откуда имеем:

(1.5)

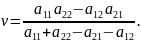
Оптимальные стратегии q₁ и q₂ определим из решения системы уравнений(1.2):

Аналогично, решая данную систему уравнений, получим:

(1.6)

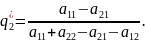
Задача

Найти оптимальную смешанную стратегию руководителя коммерческого предприятия и гарантированный средний выигрыш при выборе из двух новых технологий продажи товаров А₁ и А₂, если известны выигрыши каждого вида новых технологий продажи по сравнению со старыми технологиями В₁ и В₂, которые представлены в виде матрицы:

	0,3	0,8
	0,7	0,4

Решение

			αi
	0,3	0,8	0,3
	0,7	0,4	0,4
βj	0,7	0,8

Имеем, , . Так как α < β игра не имеет решения в чистых стратегиях и седловой точки нет.

Решение в смешанных стратегиях для игрока А (новые технологии) находим по формулам (1.5)

, ν=0,55

Выводы для А:

Коммерческое предприятие получит гарантированный средний выигрыш 0,55 усл. ед., если будет использовать новую технологию продажи с вероятностью 37,5%, а новую технологию с вероятностью 62,5%

Решение в смешанных стратегиях для игрока В (старые технологии) находим по формулам (1.6)

, ν=0,55

Выводы для В:

Коммерческое предприятие не получит проигрыш больше чем 0,55 усл. ед., если будет использовать старую технологию продажи В₁ с вероятностью 50%, а старую технологию В₂ с вероятностью 50% .