38

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Финансовый университет

при Правительстве Российской Федерации»

Орловский филиал

Кафедра «Математика, информатика и общегуманитарные дисциплины»

Е.Т. Коковин

Теория игр

Методические указания по выполнению контрольной работы

Для студентов, обучающихся по направлению подготовки

38.03.01 «Экономика»

(заочная форма обучения, в т.ч. на базе высшего образования)

Орел – 2017

Методические указания обсуждены

на заседании кафедры «Математика, информатика и общегуманитарные дисциплины»

(Протокол № 1 от 12 сентября 2017 г.)

Зав. кафедрой – кандидат физико-математических наук, доцент

Е.С. Филонова

Содержание

Введение……………………………………………………………………………3

1.2 Решение игр в смешанных стратегиях 9

Глава 3. Задания для выполнения контрольной работы 32

3.1. Порядок выполнения и оформления контрольной работы 33

3.2. Задания контрольной работы 34

Учебно-методическое и информационное обеспечение дисциплины 39

1. Литература 39

Глава 1. Матричные игры 4

1.1. Решение игр в чистых стратегиях…………………………………….…4

1.1.1 Редукция матричной игры……………………………………………..5

1.1.2 Аффинное правило……………………………………………………..7

1.2 Решение игр в смешанных стратегиях …9

1.2.1 Аналитическое решение матричной игры 2х2………………………10

1.2.2 Графическое решение матричной игры 2х2………………………….12

1.2.3 Матричные игры 2xn…………………………………………………..13

1.2.4 Матричные игры mx2………………………………………..………..16

1.2.5. Сведение конечной матричной игры к задаче линейного

программирования…………………………………………………………. 19

Глава 2. Игры с природой……………………………………………………….23

2.1 Понятие игры с природой……………………………………………….23

2.2 Доминирование (мажорирования) в играх с природой……………...24

2.3 Игры с природой в условиях полной неопределенности.................24

2.4 Игры с природой в условиях риска…………………………………...29

Глава 3. Выполнение контрольной раоты………………………………………32

3.1. Порядок выполнения и оформления контрольной работы…………..32

3.2. Задания контрольной работы…………………………………………..33

Учебно-методическое и информационное обеспечение дисциплины………..38

Введение.

На практике при рассмотрении экономических задач приходится принимать решения в условиях неопределен­ности, т.е. когда две (или более) сторо­ны преследуют различные цели, а результаты любого действия каждой из сторон зависят от действий партнера. В экономике конфликтные ситуации встречаются часто и имеют многообразный характер. К ним относятся, например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Во всех этих при­мерах конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптималь­ные решения, которые реализуют поставленные цели в наиболь­шей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера, и учитывать неиз­вестные заранее решения, которые эти партнеры будут прини­мать.

Для решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разра­ботаны математической теорией конфликтных ситуаций, которая носит название теория игр.

1. Матричные игры.

1.1 Решение игр в чистых стратегиях.

Рассмотрим конечную матричную игру двух лиц, представленную матрицей выигрышей (mxn), где число стратегий игрока А совпадает с числом строк i=1,…,m, а число стратегий игрока В совпадает с числом столбцов j=1,…,n.

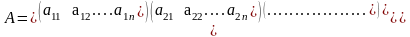
Игрок А придерживается максиминной стратегии. Он хочет получить гарантированный выигрыш. Это значит, что для каждой i-ой стратегии он определяет наименьшее значение своего выигрыша, а затем выбирает максимальное из них. Математически максиминную стратегию можно записать в виде

Игрок В придерживается минимаксной стратегии. Он своими оптимальными стратегиями стремится уменьшить выигрыш игрока А. Поэтому при каждой j-ой стратегии он определяет величину своего мах проигрыша, а затем выбирает минимальный из них. Математически минимаксную стратегию можно записать в виде

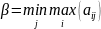
Если выполняется равенство α = β, то игра имеет оптимальное решение в чистых стратегиях и чистая цена игры ν равна

ν = α = β.

В этом случае игра называется игрой с седловой точкой.

Если имеет место неравенство α < β, то игра не имеет решения в чистых стратегиях, а цена игры удовлетворяет неравенству

α < ν < β

В этом случае игра не имеет седловой точки, но имеет решение в смешанных стратегиях.

Задача.

Дана платежная матрица игры. Определить верхнюю и нижнюю цены игры, также минимаксную и максиминную стратегии игроков.

	B1	B2	B3	αi
A1	1	2	3	1
A2	4	5	6	4
βj	4	5	6

Решение.

1) Нижняя цена игры.

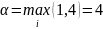, следовательно, максиминная стратегия А₂

2) Верхняя цена игры.

, следовательно, максиминная стратегия В₁

Имеем, ν = α = β = 4 – чистая цена игры при стратегиях А₂ и В₁

Следовательно, это игра с седловой точкой и есть решение в чистых стратегиях.

Решение игры: оптимальные чистые стратегии (А₂, В₁), цена игры ν = 4.