1.5 Термодинамический анализ возможности протекания химического процесса

Изменение энергии Гиббса и Гельмгольца служит критерием направления самопроизвольного процесса в закрытых системах.

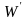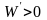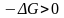При осуществлении самопроизвольного процесса система в состоянии произвести работу . При этом и, следовательно, . Отсюда вытекает очень важное соотношение, которое является критерием возможности самопроизвольного протекания потекания процесса в закрытой системе в изобарно-изотермических условиях:

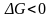(при p = const и T = const)

Аналогично можно показать, что в изохорно-изотермических условиях критерием возможности самопроизвольного процесса является:

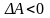(при V = const и T = const)

Таким образом, в закрытых системах, какими являются большинство химико-технологических систем, ответ на этот вопрос получают на основании изменения энергии Гиббса или энергии Гельмгольца:

В закрытых системах самопроизвольные процессы могут протекать только в направлении уменьшения энергии Гиббса (при p = const и T = const) или энергии Гельмгольца (при V = const и T = const), а в состоянии равновесия эти функции имеют минимальное значение.

1.6 Химическое равновесие

Многие химические процессы в химико-технологических системах являются двусторонними – они могут протекать как в прямом, так и в обратном направлении. Скорость химических реакций пропорциональна концентрации реагентов. Для большинства реакций скорость прямой реакции падает во времени, а скорость обратной реакции растет по мере накопления реагентов. При достижении равенства скорости прямой и обратной реакции наступает равновесие. Химическое равновесие является динамическим равновесием, при котором прямая и обратная реакция идут с одинаковыми скоростями. При этом концентрации исходных веществ и продуктов реакции не меняются и называются равновесными концентрациями.

Расчет термодинамических констант равновесия

Термодинамическая константа равновесия может быть выражена как через активности веществ, участвующих в реакции, K_a, так и через фугитивности K_f:

,

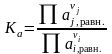
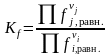Термодинамические константы равновесия являются безразмерными величинами.

Константа равновесия 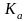может быть рассчитана по частному уравнению изотермы химической реакции:

,

(1.36)

если известно значение изменения стандартной энергии Гиббса при данной температуре. Тогда термодинамическая константа равновесия рассчитывается как экспонента:

,

Термодинамическая константа равновесия зависит от природы реагирующих веществ и температуры, но не зависит от давления, поскольку изменение стандартной энергии Гиббса не зависит от давления по определению.

Величина константы равновесия может принимать значения от нуля до бесконечности:

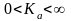
Пример: Рассчитаем термодинамическую константу равновесия реакции синтеза метанола при температурах 298 и 1000 К и давлении 101,325 кПа.

Решение: Рассчитаем изменение стандартной энергии Гиббса при температуре 298К, используя рассчитанные в предыдущих примерах значения 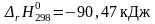и :

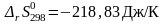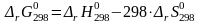= – 90,47∙10³ – 298∙( – 218,83) = – 25258,66 Дж

По частному уравнению изотермы химической реакции

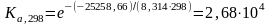
Для расчета константы равновесия при 1000 К воспользуемся рассчитанным в предыдущем примере значением стандартной энергии Гиббса при температуре 1000 К для реакции синтеза метанола .

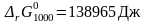По частному уравнению изотермы химической реакции

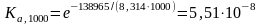
Если химическая реакция протекает при давлениях меньше ≤ 50 атм, то константа равновесия, выраженная через приведенные давления 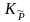, равна термодинамической константе равновесия K_a и является безразмерной величиной.

Практические константы равновесия

Химическое равновесие могут характеризовать практические константы равновесия. Практические константы равновесия могут быть рассчитаны, если при равновесии определить количества или концентрации веществ, участвующих в реакции тем или иным методом химического или физико-химического анализа. Они могут быть выражены

– через числа молей веществ n_i,j в равновесии:

;

(1.37)

– через молярные концентрации веществ с_i,j в равновесии:

;

(1.38)

– через мольные доли веществ x_i,j в равновесии:

;

(1.39)

– через парциальные давления веществ p_i,j в равновесии:

(1.40)

Практические константы равновесия являются размерными величинами.

Удобно использовать и безразмерные константы равновесия, например, константу, выраженную через приведенные давления :

,

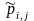(1.41)

гд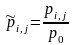е , а p₀ – стандартное давление.

Между практическими константами равновесия существует определенная математическая связь. Например, легко показать, что константа связана с практической константой равновесия, выраженной через моли K_n, следующим соотношением

(1.42)
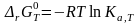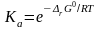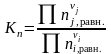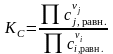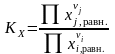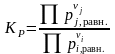
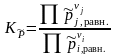